Other Advanced Control Techniques

In class activities

Activities

1. Effect of delay time on controller tuning

   Consider a process with following transfer function

   $$\begin{array}{}\text{(1)}& G_p=\frac{1}{(5s+1)(3s+1)}\end{array}$$

   The PI controller for this process has parameters of K_c = 3, and τ_I = 6.

   What happens to the response when a dead time of θ = 2 is introduced?

   Determine controller parameters to obtain an overshoot similar to the process without delay.

2. Design a Smith predictor for problem 1.

   Use problem_4_1_pure_feedback.slx as a starting point.

Solution

problem_4_1_pure_feedback.slx.

problem_4_1_smith_predictor.

3. It is desired to control the size distribution of crystals produced in vacuum continuous crystallizer, but it’s very difficult to measure i.e. requires lengthy lab test. Some experiment suggest that crystal size distribution are strongly related to the (1) stirrer speed q, (2) magma temperature T, (3) degree of supersaturation C-Cs, and (4) mother liquor density r. C is concentration of the solute and Cs is the solubility of the solute.

   1. Suggest an inferential control technique for crystal size distribution
   2. Show the schematic of the control strategy. Comment on the effectiveness of the strategy.

Solution

Use an inferential (soft‑sensor) MPC that estimates key crystal size metrics from easily measured variables, then controls them.

Primary CV: median size $d_{50}$. Additionally, the CoV (coefficient of variance) of the crystal size distribution (CSD) can also be calculated.

Build a soft sensor to estimate $d_{50}$ and CoV from $q$ (stirrer speed), $T$ (magma temperature), $S=C-C_s(T)$ (supersaturation), and $\rho$ (mother‑liquor density). The soft sensor can be built using a data driven model or a mechanistic first principles model.

Manipulated variables: * coolant or steam valve that sets temperature, hence $C_s(T)$ and $S$ * vacuum or condenser duty that sets boiling rate and $T$ * seed addition rate or seed PSD * feed concentration or solvent/antisolvent addition that sets $C$ and $\rho$ * agitator speed $q$ within mechanical limits

Disturbance variables: feed rate, impurities, mother‑liquor recycle.

Control strategy:

• Tight PID feedback loops for T, P, and q.
• MPC is used to adjust the setpoint
• Optionally, a additional control loop on $\rho$ via solvent/ purge flow rate control.

Limitations:

• Model mismatch
• Sensor quality/ accuracy
• Requires periodic lab data for bias correction

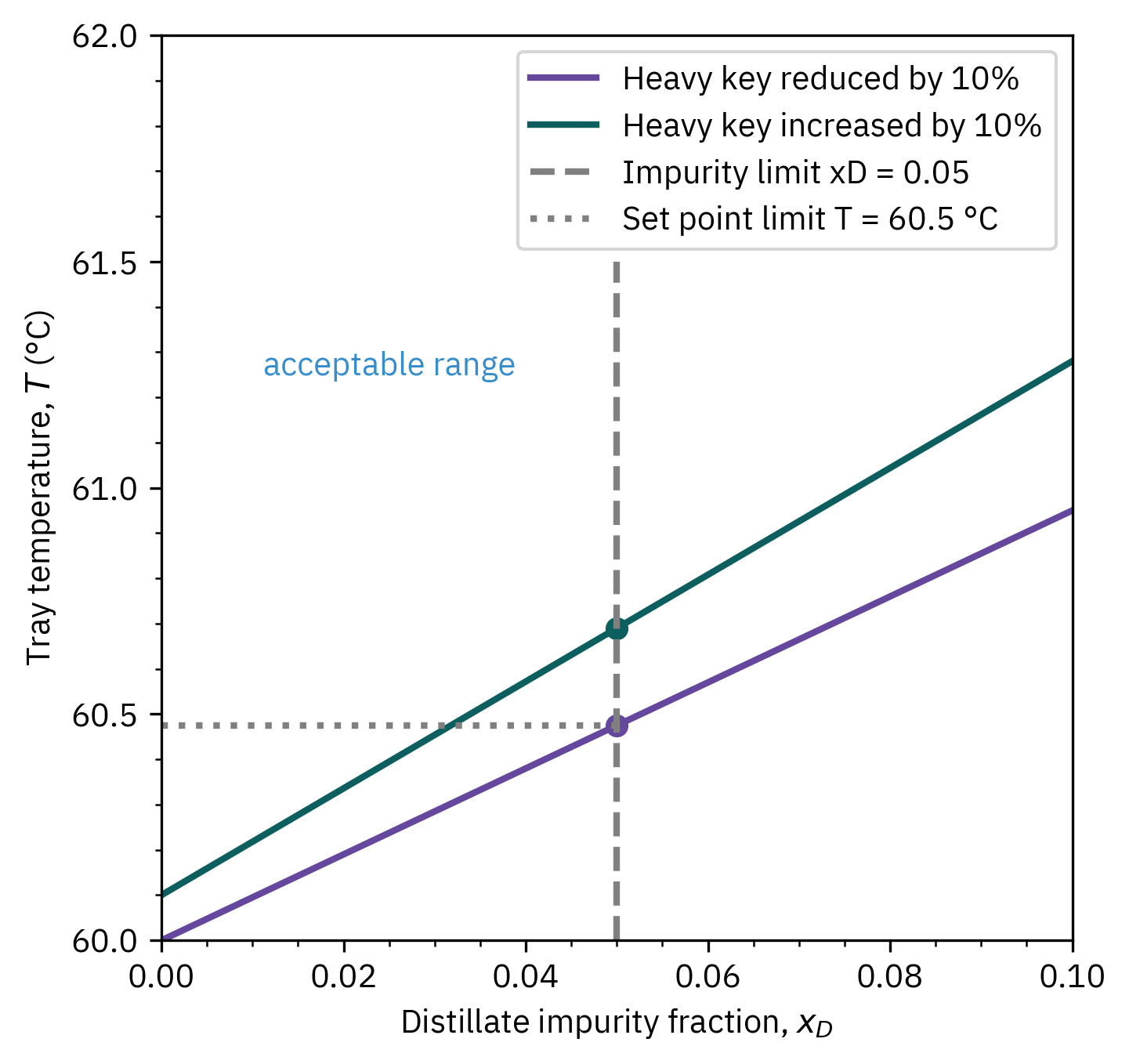
4. Consider two inferential model for the prediction of distillation top impurity fraction xD and a tray temperature T as follows: Reduction in the heavy key fraction in the feed by 10%:

   $$\begin{array}{}\text{(2)}& T=60+9.5x_D;0\le x_D\le 0.1\end{array}$$

   Increase in the heavy key fraction in the feed by 10%:

   $$\begin{array}{}\text{(3)}& T=60.1+11.8x_D;0\le x_D\le 0.1\end{array}$$

   To ensure that that the impurity in the distillate remains within 5%, what would be the setpoint to the inferential tray temperature controller? Explain how you would determine the appropriate setpoint value.

Solution

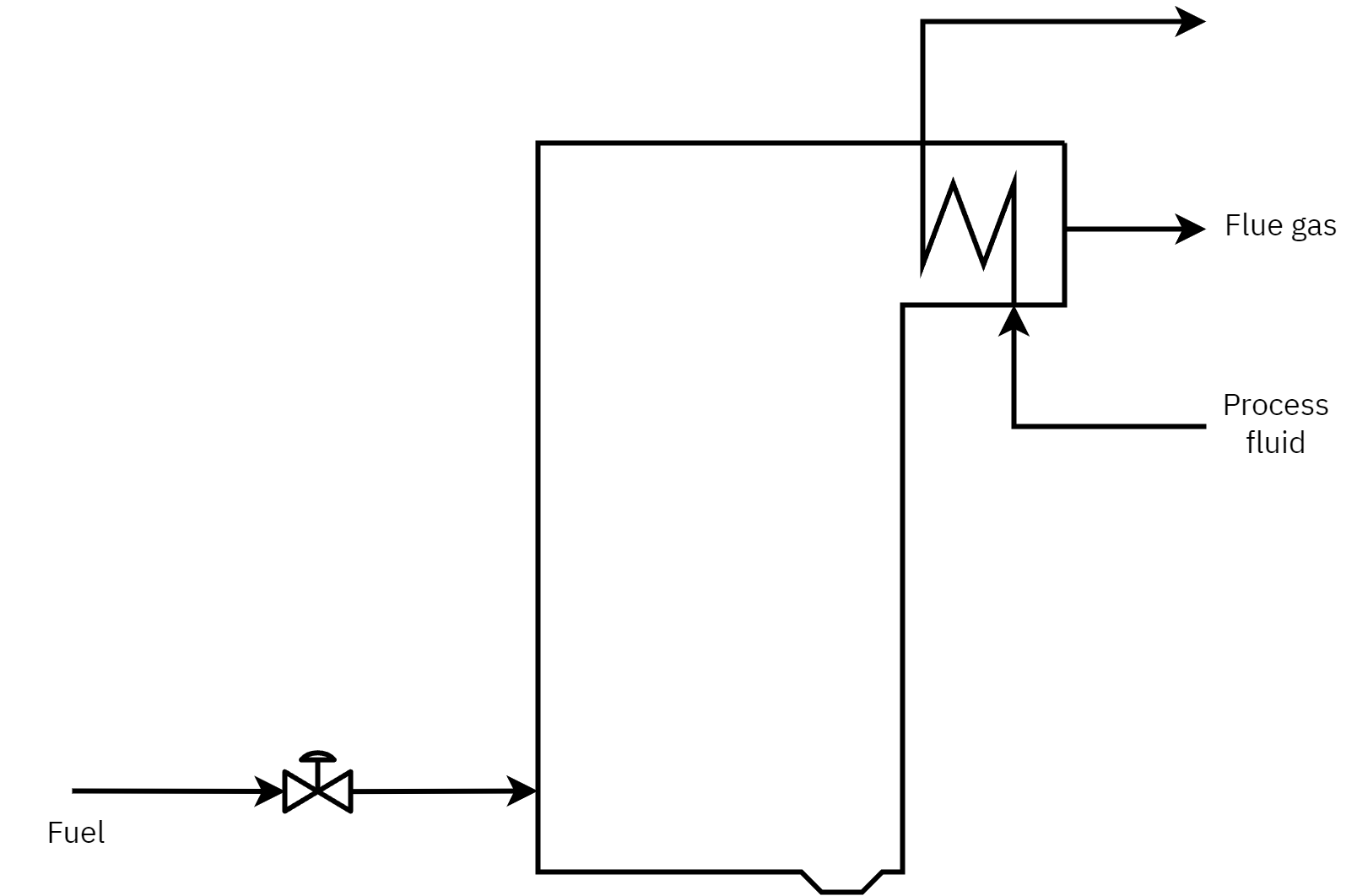
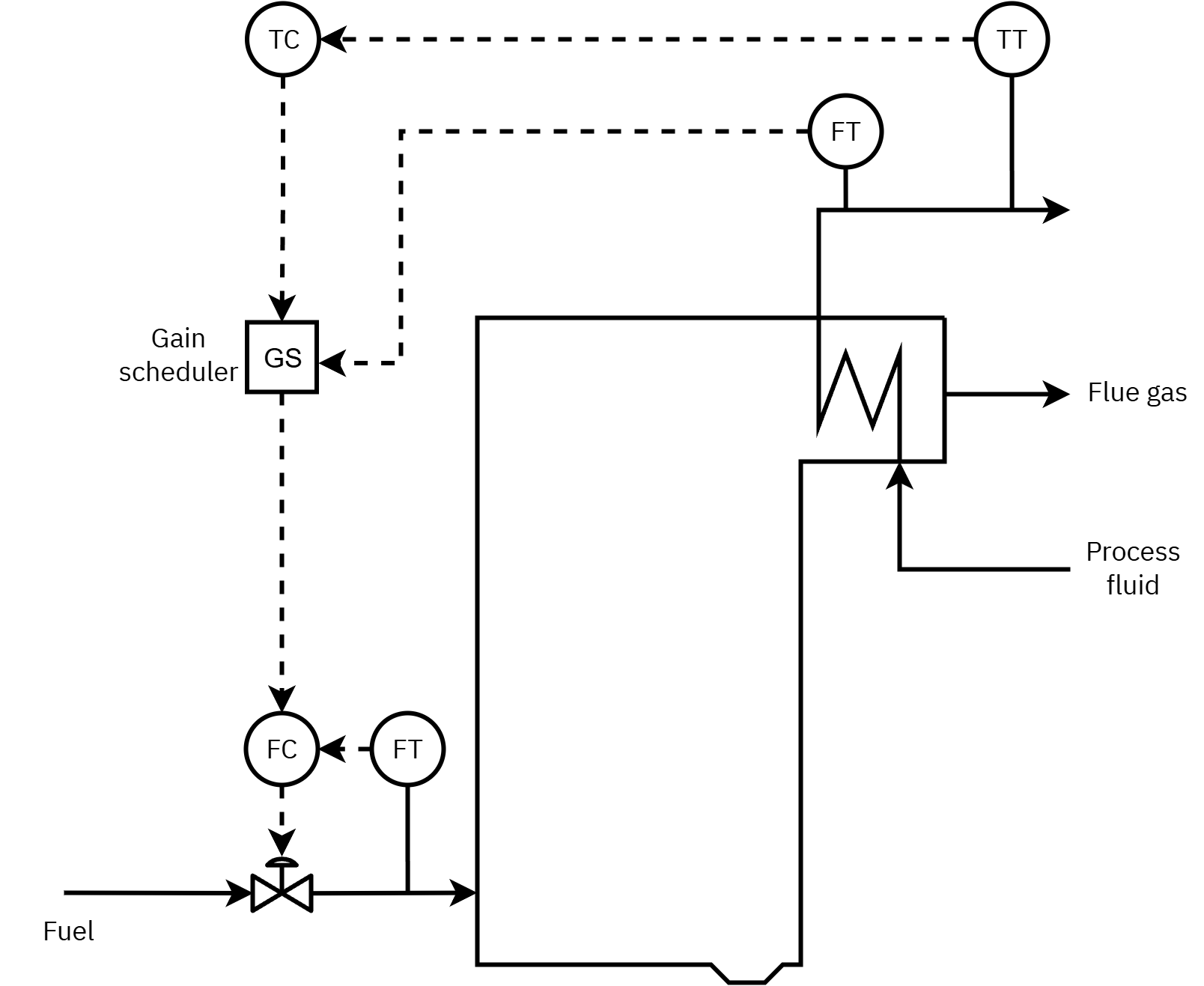
5. Gain Scheduling: For the furnace shown in Figure 1, show a schematic control strategy with gain scheduling. What variable can you use for gain scheduling? Give your reasons.

Figure 1: Furnace

Solution

Figure 2: Furnace gain scheduling

6. A cold process fluid is heated up in a shell-and-tube heat exchanger using steam. At the nominal process feed flow rate, the transfer function of the exit temperature of the process fluid is given as follows:

   $$\begin{array}{}\text{(4)}& G_p=\frac{exp(-2s)}{(5s+1)}\end{array}$$

   It has been found that the process gain is strongly related to the process fluid flow rate given as follows:

   $$\begin{array}{}\text{(5)}& K_p=1+0.5\mathrm{\Delta }{F}_p\end{array}$$

   Where, ΔF_p denotes the change of process fluid flow rate from its nominal value, i.e., $\mathrm{\Delta }{F}_p=F_p-{\overline{F}}_p$ where $F_p$ is the current value of process fluid flow rate and ${\overline{F}}_p$ the nominal value (steady-state) of the process fluid flow rate.

   An ideal PI controller is given by

   $$\begin{array}{}\text{(6)}& G_c=K_c(1+\frac{1}{{\tau }_{I}s})\end{array}$$

   Based on the PI controller tuning via the stability-based formula,

   $$\begin{array}{}\text{(7)}& K_c=\left(\frac{r_p}{K_p}\right)\left(\frac{{\tau }_p}{{\theta }_p}\right);0<r_p<1\end{array}$$

   and

   $$\begin{array}{}\text{(8)}& {\tau }_I={\tau }_p\end{array}$$

   Assume the baseline or nominal value of the process fluid flow rate is ${\overline{F}}_p=2$, calculate the values in Table 1.

   Table 1: Tuning parameters for problem 5

   Fp	Kp	Kc
   2 (nominal)	1	1.75
   3	1.5	1.17
   1	0.5	3.5

   Note: To calculate K_c a value of r_p = 0.7 was used.

   Evaluate the controller performance. Simulink file for problem implementation without gain scheduling is given here.

Solution

PI without gain scheduling.

PI with gain scheduling.

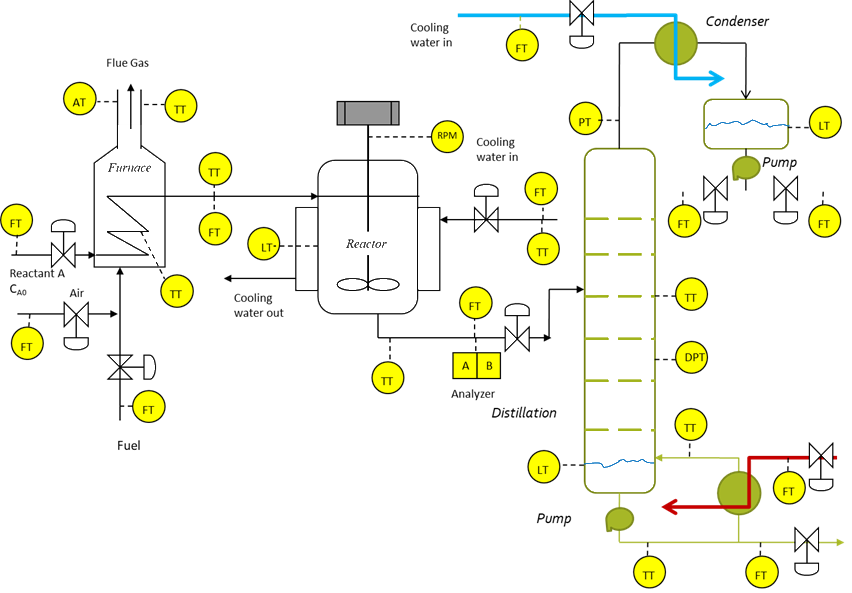
7. Reactor-Furnace-Distillation System:

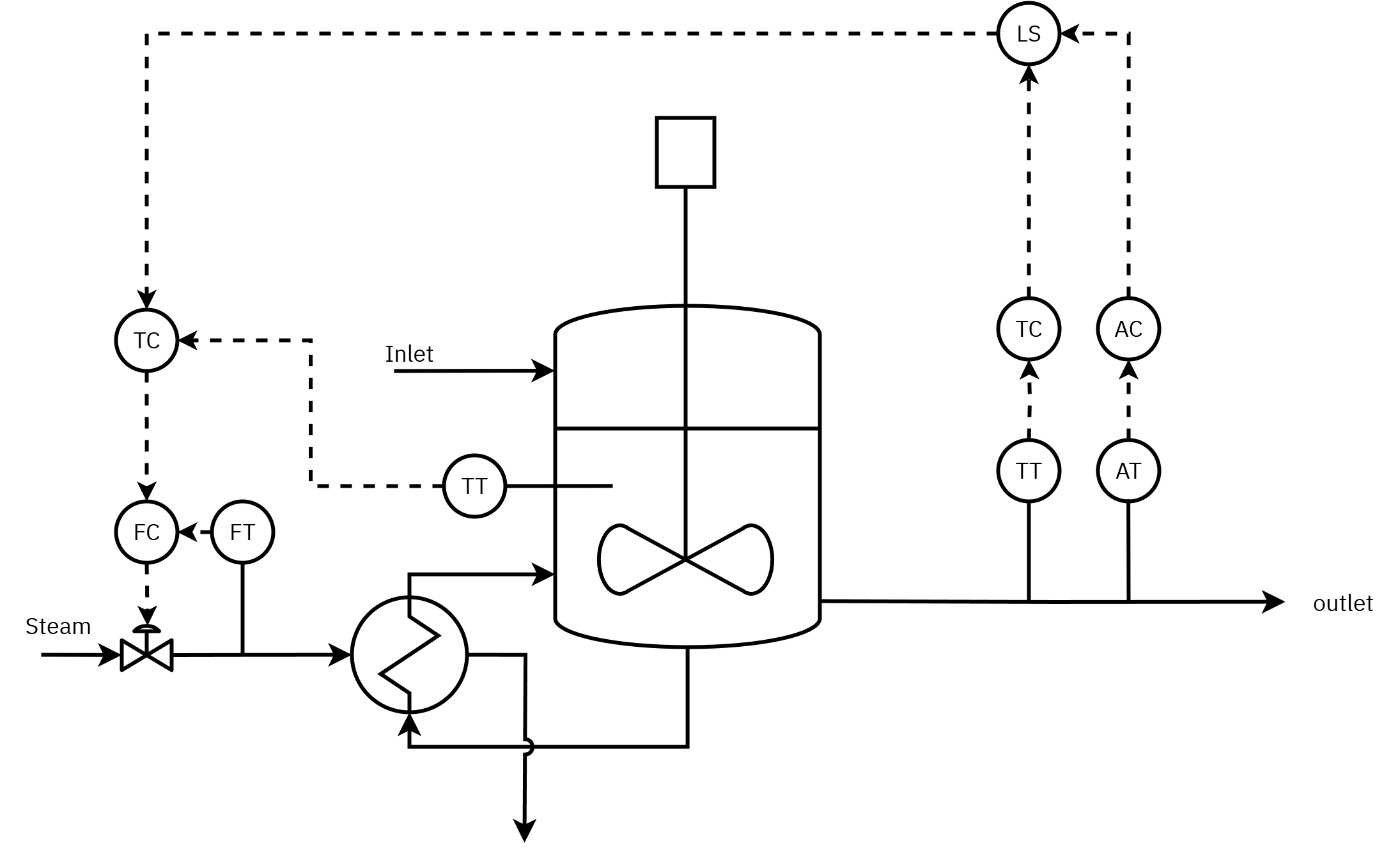
   For RFD system shown in Figure 3, draw the schematic of LS control strategy for the reactor system, where it is desired to control the component A (CA), and temperature of the reactor effluent T. The reactor temperature should not exceed Tmax due to the possibility of the process encountering runaway reaction and instability.

Figure 3: Reactor-Furnace-Distillation system

Solution

Figure 4: Reactor-Furnace-Distillation system low select control