Principal Component Analysis

Advanced Modeling and Control

Univariate vs multivariate analysis

  • Univariate statistical analysis – 1 input variable and 1 response variable
    • E.g., input variable = reactor temperature; response variable = reactor conversion
  • Multivariate statistical analysis – multiple variables and multiple responses
    • E.g., input variables = reactor temperature, feed concentration; response variables = reactor conversion and product yield
  • Multivariate analysis attempts to reveal the key information from the correlated variables
  • Widely used in the science and engineering applications – data analysis

Multivariate analysis

  • Goal of many multivariate approaches is simplification – from large dimension to smaller or reduced dimension of datasets
  • Such approaches are exploratory, e.g., generate hypotheses rather than for testing them
  • Some approaches:
    1. Discriminant Analysis – identifying the relative contribution of 𝑝 variables to separation of the groups
    2. Principal Component Analysis (PCA) – reduces large dimension of a data set to smaller dimension
    3. Multivariate regression, e.g., partial least square (PLS) regression

Discriminant analysis

  • Discriminant analysis (DA) is a supervised learning technique primarily used for classification tasks. It seeks to find the combination of features that best separates or discriminates between two or more predefined classes.

  • Objective is to find a linear combination of features that best separates two or more classes.

  • Discriminant Function: A function created from the linear combination of predictor variables that best separates the classes.

  • Decision Boundary: The line or surface that separates different classes in the feature space.

  • Advantages

    • Simple and easy to understand.
    • Effective when data meets the assumptions of normality and equal covariance matrices.

  • Disadvantages

    • Assumes linear class boundaries, which may not perform well with non-linear separations.
    • Sensitive to outliers, which can significantly impact results.

Applications of discriminant analysis

  • Fault Detection and Diagnosis

    DA can be used to distinguish between normal reactor operation and issues like overheating, catalyst deactivation, or abnormal pressure drops by analyzing sensor data.

  • Quality Control

    In polymer production, DA can help in assessing product quality through variables such as molecular weight, viscosity, and tensile strength.

  • Predictive Maintenance

    For heat exchangers, DA can identify operational states, ranging from “normal” to “early fouling” or “severe fouling,” allowing for timely maintenance.

  • Safety and Risk Management

    DA can be used to provide early warnings by classifying real-time plant conditions as safe or potentially hazardous, enabling preventive actions.

Principal component analysis

  • An exploratory technique used to reduce the dimensionality of the data set to 2D or 3D

  • Can be used to:

    • Reduce number of dimensions in data: Minimizes the number of variables in a dataset, helping in data simplification

    • Identify outliers

    • Find patterns in high-dimensional data: Identifies underlying patterns in high-dimensional data, making it easier to analyze.

    • Visualize data of high dimensionality: Facilitates the visualization of complex, high-dimensional datasets by projecting them into lower dimensions.

    • Example applications:

      • Process monitoring, quality control
      • Environmental analysis
      • Face recognition, image compression
      • Gene expression analysis

What are Principal Components?

  • Suppose you have a dataset with many variables (features), say 10, 50, or even 100 dimensions.

    • Each data point in this high-dimensional space is an observation or a sample, characterized by these variables.

  • PCA transforms this high-dimensional data into a new set of axes called principal components.

  • These are linear combinations of the original variables.

  • The principal components are ordered by the amount of variance they explain:

    • First Principal Component (PC1): The direction in the data that captures the most variance (i.e., the greatest spread of the data).

    • Second Principal Component (PC2): The direction orthogonal (at a right angle) to PC1 that captures the next highest amount of variance.

PCA analysis

  • PCA decomposes a data set \bf{X}[matrix (m observations, n variables)] into

    \bf{X} = \bf{TP^T} + \bf{E}

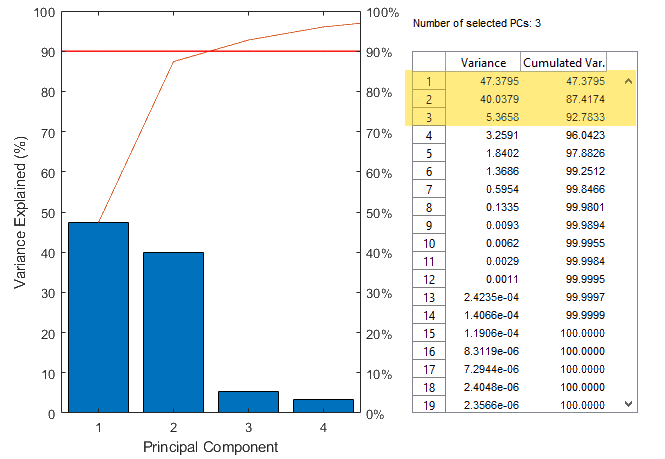
    • k is the number of principal components (typically k \le n)

    • \bf{T} is the scores matrix (order m \times k).

      Scores are the projections of the original data onto the principal components. Each row represents an observation’s coordinates in the reduced k-dimensional space.

    • \bf{P} is the loading matrix (order n \times k).

      These are the coefficients that define each principal component as a linear combination of the original variables. Each column represents a principal component, and each row corresponds to a variable.

    • \bf{E} is the residual or error matrix (order m \times n).

      Ideally, if all principal components are retained, \bf{E} would be a zero matrix. In practice, it captures the noise or less important variations in the data that are not accounted for by the principal components.

  • Principal components are orthogonal to each other, i.e., they are uncorrelated

  • \bf{P} can be obtained using the singular value decomposition (SVD) or ALS (alternate least square).

PCA analysis

  • Principal components show directions of the data that explain a maximal amount of variance

  • The larger the variance carried by a line, the larger the dispersion of the data points along it

  • Original data on the left with original coordinate x_1 and x_2

  • Variance of each variable graphically represented

  • Direction of the maximum variance i.e., principal component PC1 and PC2

Process modeling using PCA

Distillation column example

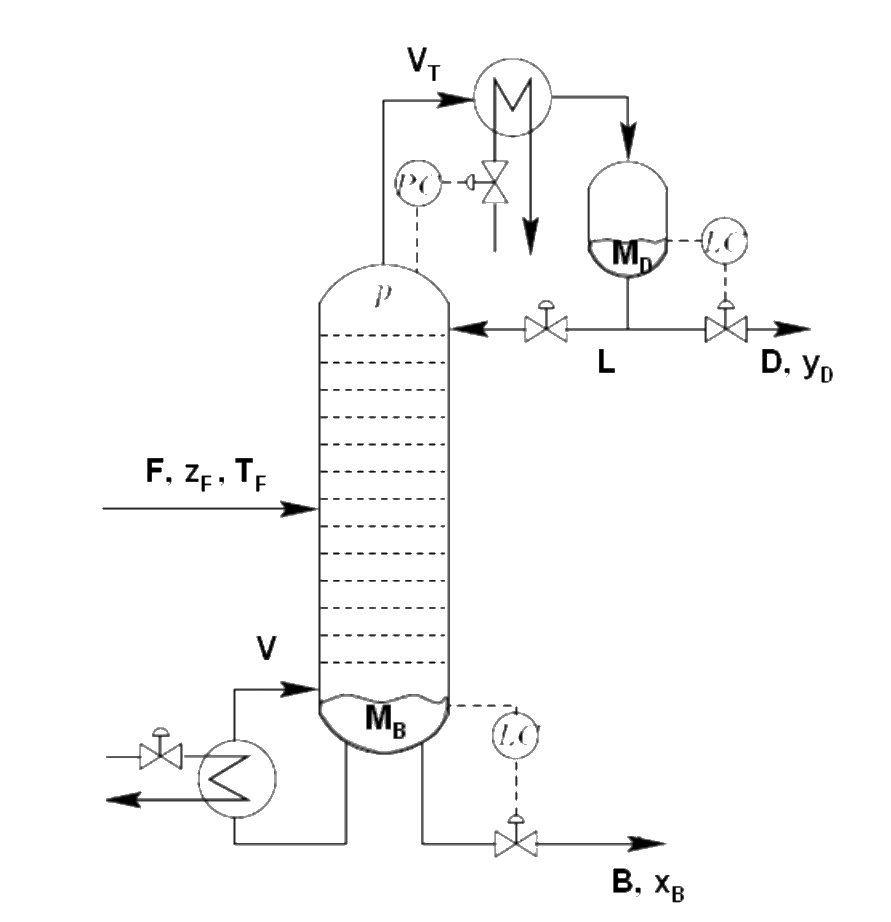
  • Separating a Methanol — Ethanol mixture

  • CVs: Y_D, X_B; MVs: D, B, L, V; DVs: F_T z

  • SISO control

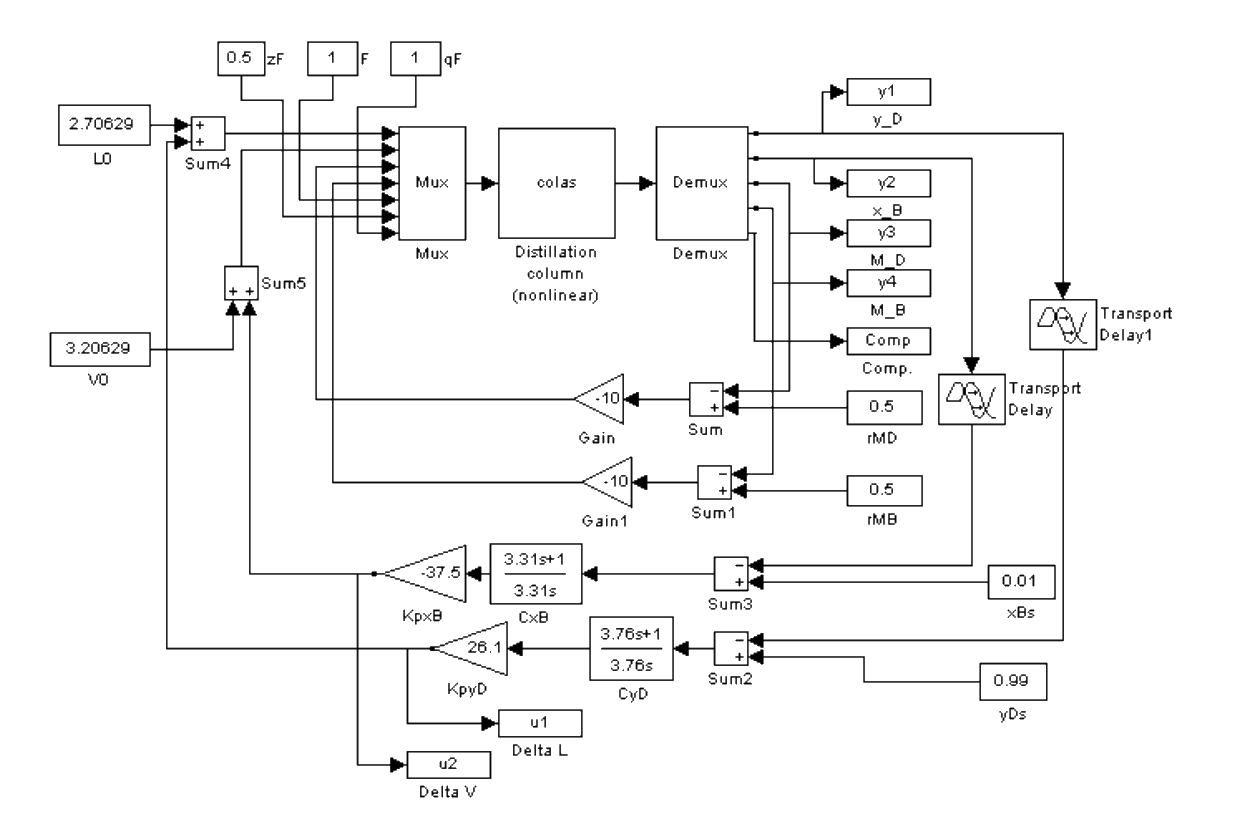
  • Model and data set incorporated in app

  • Workflow

    • Phase I: Model steady state with PCA
    • Phase II: Project new observations on model and detect deviation

Phase I: Model steady state with PCA

  • Phase I: Model building to capture normal operating conditions
  • No plant data \rightarrow use Simulink model to generate process data

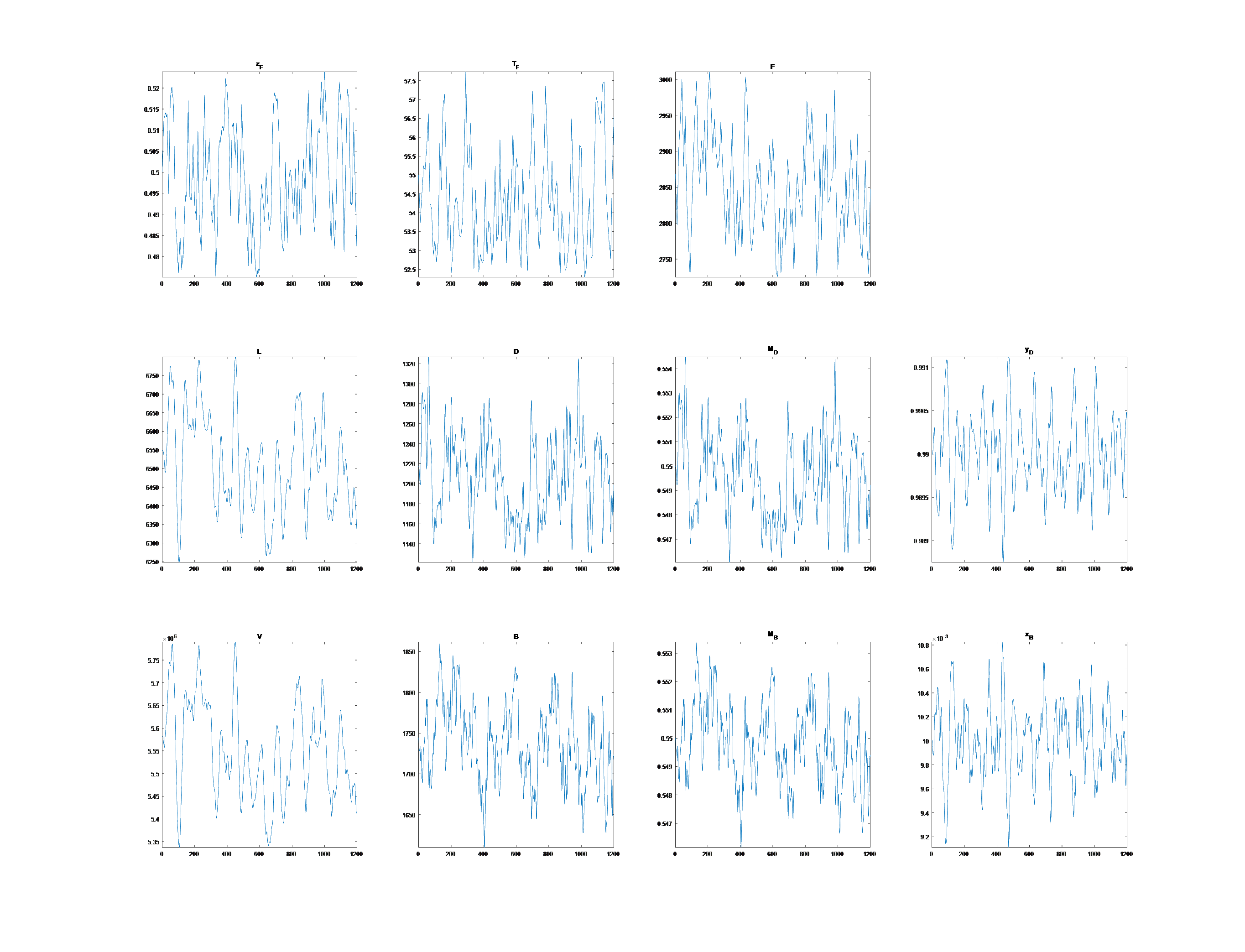
Phase I: Model steady state with PCA

  • Reduce size of data set
    • Higher observations means better model but increases computing requirement
  • Derive PCA model based on smallest data set that represents information in entire data set
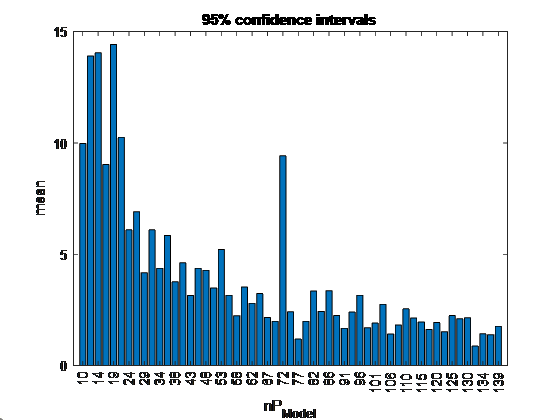
    • Select random subset
    • Fit PCA model
    • Compute percentage of out-of-control points
    • If below threshold (5%), stop or else repeat above steps by increasing size of random subset

Phase I: Model steady state with PCA

Phase I: Model steady state with PCA

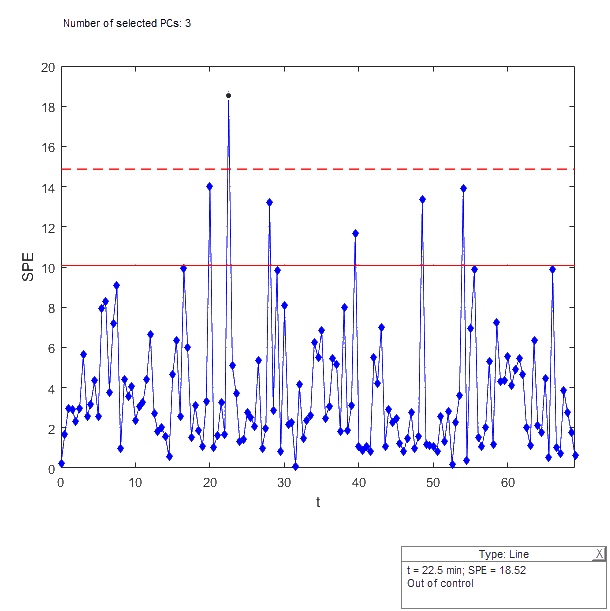
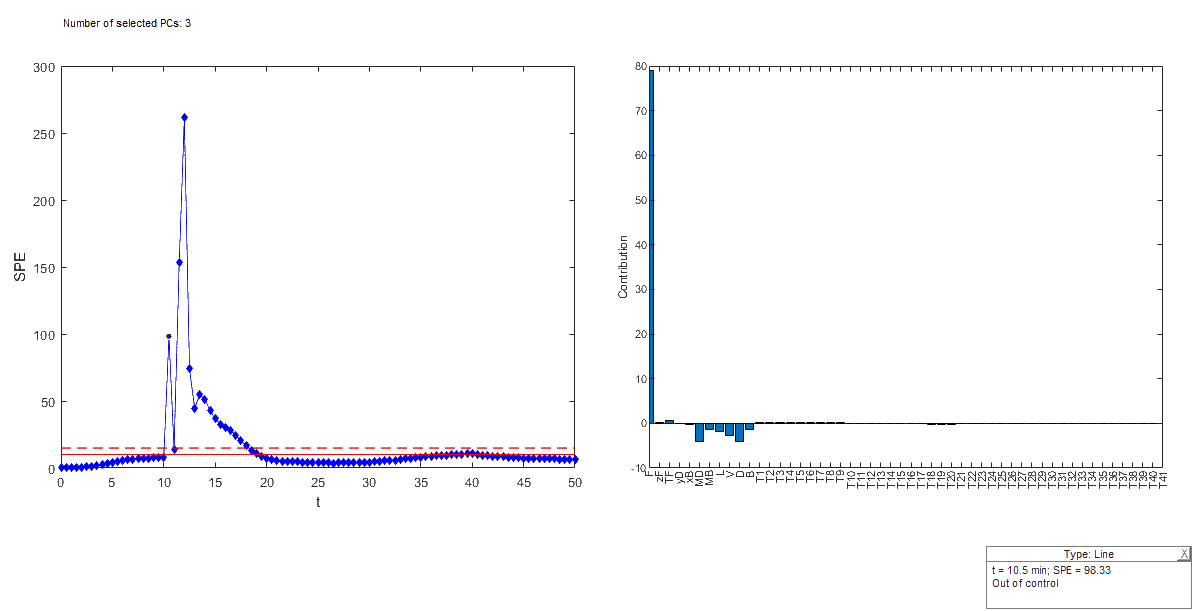
SPE control chart

  • Measures the distance to the model

Hotelling’s T^2 control chart

  • Measures if the projected observations are in NOC zone

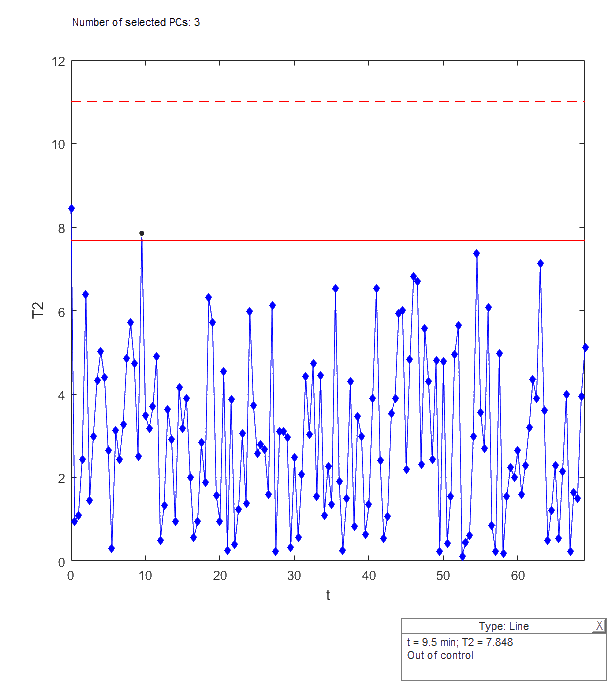
  • Solid red line indicates 90% confidence interval; dashed red line indicates 95% confidence interval.

Phase II: Model exploitation

  • New ‘faulty’ data is pre-processed and projected onto the PCA model

  • If process is below control limits in both charts Process under control

  • If point is outside limits

    • Check SPE chart and look at corresponding contribution plots
    • Check T2 chart and look at corresponding contribution plots

  • Faults

    • Pl loop failure

    • Operating mode change

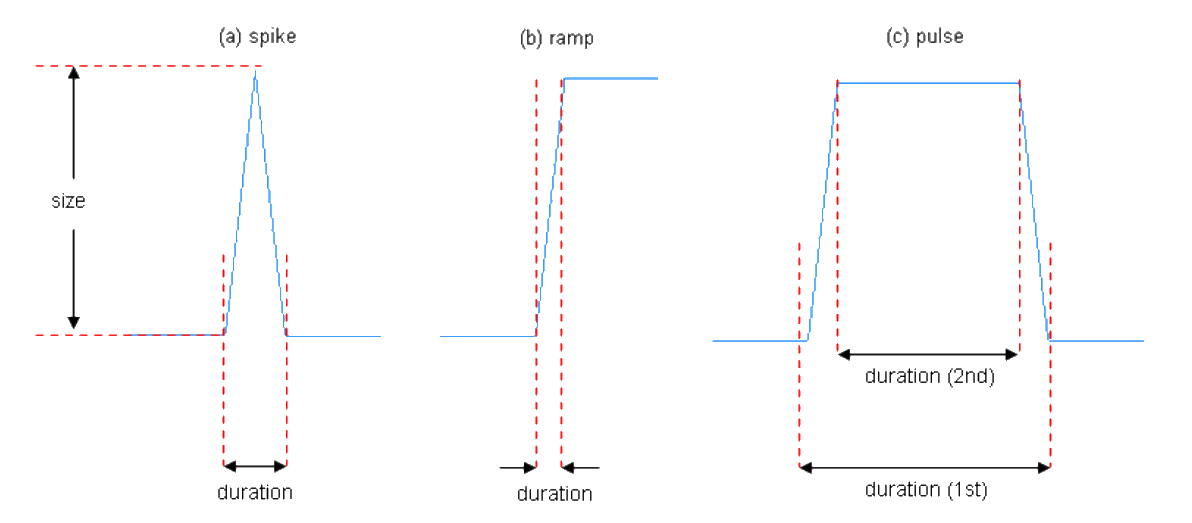
    • 3 types of process disturbance: spike, ramp, pulse

Contribution chart

  • Shows how each original variable contributes to a particular principal component

  • Helps to identify which variables are most responsible for the patterns or outliers

  • Variables with higher contributions are those that have a stronger influence on the differentiation of the observations.

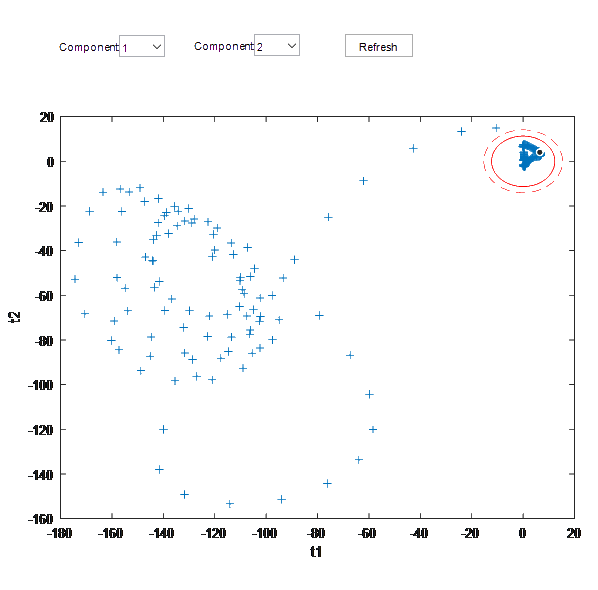
Scores

  • Score plot typically represents the data points projected onto the first two principal components.

  • Each point represents an observation (e.g., a sample or an experiment) in the reduced dimensionality space.

  • The score plot is used to identify patterns, groupings, or outliers in the data.

Partial least square (PLS) regression

PCR

  • Unsupervised learning: PCR finds new directions (PCs) that best summarize the features (variables) X_1, \ldots, X_M

  • The PCs that best explain the features might not be the best for predicting the response.

  • Not considering the response Y may lead to PCs that don’t help in predicting Y.

  • The directions that best describe the features might not be the best for prediction.

PLS

  • Supervised learning: PLS reduces dimensions but does so by considering the response Y while finding new directions Z_1, \ldots, Z_M

  • Z_1, \ldots, Z_M are the linear combinations of original features.

  • This means the new features are not only good approximations of the original ones but are also related to the response.

pls model

  • Multivariate model

    X = T P^T + E_X, \qquad Y = U Q^T + E_Y

    • X \in \mathbb{R}^{n \times m} matrix of predictors, T \in \mathbb{R}^{n \times l} matrix of projections of X (scores)

    • P \in \mathbb{R}^{m \times l} orthogonal loading matrix, E_X \in \mathbb{R}^{n \times m} error matrix

    • Y \in \mathbb{R}^{n \times p} matrix of responses, U \in \mathbb{R}^{n \times l} matrix of projections of Y (scores)

    • Q \in \mathbb{R}^{m \times l} orthogonal loading matrix, E_Y \in \mathbb{R}^{n \times p} error matrix

    • Notation \mathbb{R}^{n \times p} denotes a matrix with n number of rows (observations) and p number of columns (responses).

    • m: The number of predictors (independent variables) in the matrix X

    • l: The number of latent variables or components extracted by the PLS model.

PLS model

  • T (the score matrix for X) and U (the score matrix for Y) are calculated by projecting the original matrices X and Y onto latent variables. These latent variables are found by maximizing the covariance between the projections of X and Y.

  • P (the loading matrix for X) and Q (the loading matrix for Y) are determined by regressing the original matrices X and Y onto the score matrices T and U, respectively. The loading matrices capture the relationships between the original variables and the latent variables (scores).

  • E_X and E_Y represent the residual matrices for X and Y, respectively. They capture the variation in the original matrices X and Y that is not explained by the model. These matrices are determined by subtracting the product of the score and loading matrices from the original matrices: E_X = X - TP^T and E_Y = Y - UQ^T.

  • The iterative process continues until a satisfactory number of latent variables (components) have been extracted, providing a balance between model accuracy and complexity.

Satisfactory number of latent variables

  • Cross-Validation: Split the data into training and validation sets. Increase the number of components until the prediction error on the validation set stops improving. The optimal number of components is where the validation error is minimized.

  • Explained Variance: Choose the number of components that achieve a significant portion of explained variance (e.g., 90-95%), adding more only if necessary.

  • Model Stability: Monitor model parameters (e.g., loadings and scores) as components are added. A satisfactory number is reached when these parameters stabilize, indicating no overfitting.

  • Interpretability: Choose the fewest components that offer meaningful and distinct interpretations in the context of the problem. Avoid adding components that don’t improve interpretability.

  • External Validation: Validate the model on independent data, selecting the fewest components that ensure good predictive performance and generalization.

  • Typically, cross-validation combined with explained variance is used to determine the optimal number of components, balancing model complexity, accuracy, and interpretability.

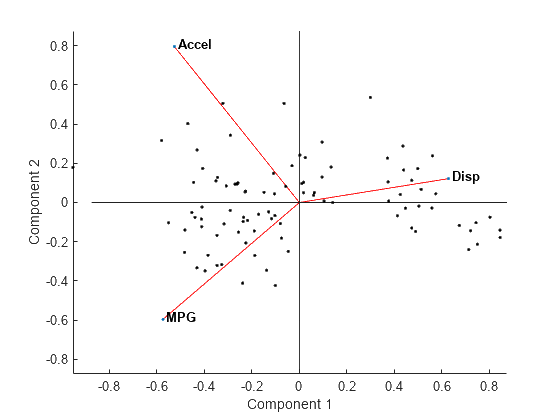
Biplot

  • The points in the biplot represent the samples projected onto the principal components (in PCA) or latent variables (in PLS).

  • The position of each point reflects how the sample is related to the components.

  • The vectors or arrows represent the original variables. The direction and length of each vector indicate the contribution of the variable to the components. Longer arrows suggest a stronger influence on the corresponding component. Variables that are closer to the origin have less influence on the components

  • Smaller angles between vectors suggest higher positive correlation, whereas angles close to 180° suggest a negative correlation.

Variable importance in projection (VIP) score

  • Identifying the most influential variables in the model

  • Shows the VIP scores, which are metrics that quantify the contribution of each variable to the model across all components

  • A common threshold is a VIP score of 1. Variables with VIP scores greater than 1 are generally considered significant contributors to the model, while those with scores below 1 may be considered less important.

  • Variables with high VIP scores are essential in explaining the variation in the dependent variable. They have a strong influence on the model’s predictions.

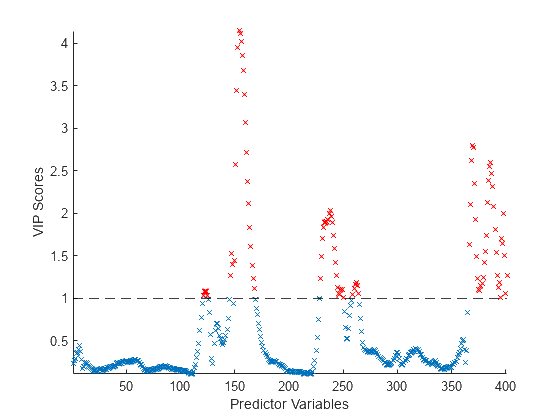
The VIP score plot can guide the selection of variables when refining a model, helping to focus on the most informative predictors.

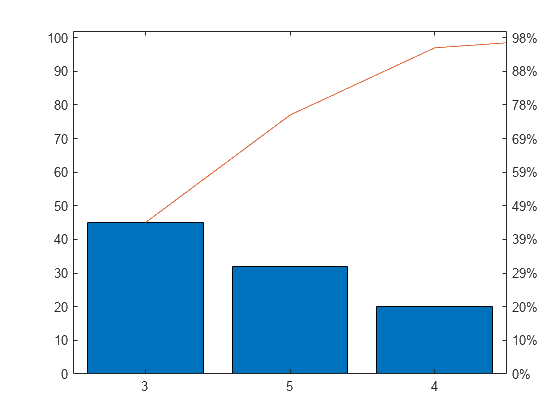
Pareto plot

  • Pareto principle (80/20 Rule): roughly 80% of the effects come from 20% of the causes.

  • The x-axis lists the different categories, arranged in descending order of their impact or frequency. Left y-axis shows the frequency, right y-axis shows the cumulative percentage.

  • Bars (Frequency/Impact): The bars represent the individual factors or categories.

    • Ordered from the most significant (highest frequency or impact) to the least significant.

  • Cumulative Line: cumulative percentage of the total impact or frequency

PLS in Matlab

  • MATLAB function called plsregress

  • [XL,YL,XS,YS,BETA,PCTVAR,MSE,stats] = plsregress(X,Y,ncomp) returns

    • The predictor and response loadings XL and YL

    • The predictor scores XS. Predictor scores are PLS components that are linear combinations of the variables in X.

    • The response scores YS. Response scores are linear combinations of the responses with which the PLS components XS have maximum covariance.

    • The matrix BETA of coefficient estimates for the PLS regression model.

    • The percentage of variance PCTVAR explained by the regression model.

    • The estimated mean squared errors MSE for PLS models with ncomp components.

    • A structure stats that contains the PLS weights, T^2 statistic, and predictor and response residuals.

Data quality

  • Data quality is crucial for developing accurate and reliable data-driven models like ANN, PLS, and others.

  • The quality of data is influenced by factors such as how it is generated, the sampling period, the number of observations, and the presence of missing data.

  • A large sampling period can lead to a significant loss of information, negatively impacting the model’s performance.

  • A short sampling period captures more detailed information, increasing the number of data points, which can strain storage and processing capacity but doesn’t necessarily increase the dimensionality of the feature space.

  • Missing data and inconsistencies can skew model training, leading to unreliable predictions and conclusions.

  • In practice, a balance must be struck between preserving information and managing storage and processing capacity to ensure both model performance and efficiency.

Summary

  • Process plant monitoring is essential for safe and profitable operations.

  • Early detection of faulty sensors or process abnormalities enhances safety and profitability.

  • Technological advances have increased data acquisition, leading to large datasets.

  • Large datasets often include irrelevant information; effective data modeling can help isolate the key variables and enhance predictions.

  • Effective data modeling with techniques like PCA and PLS helps identify key variables, predict important outcomes, and improve system interpretation.

  • Principal Component Analysis (PCA): Reduces dataset dimensionality by projecting data onto principal component space (latent variables). Widely used in the process industry.

  • Partial Least Squares (PLS): Aligns predictor and response variables in latent space, maximizing the correlation between them to improve model accuracy and system interpretation.

Advanced Modeling and Control