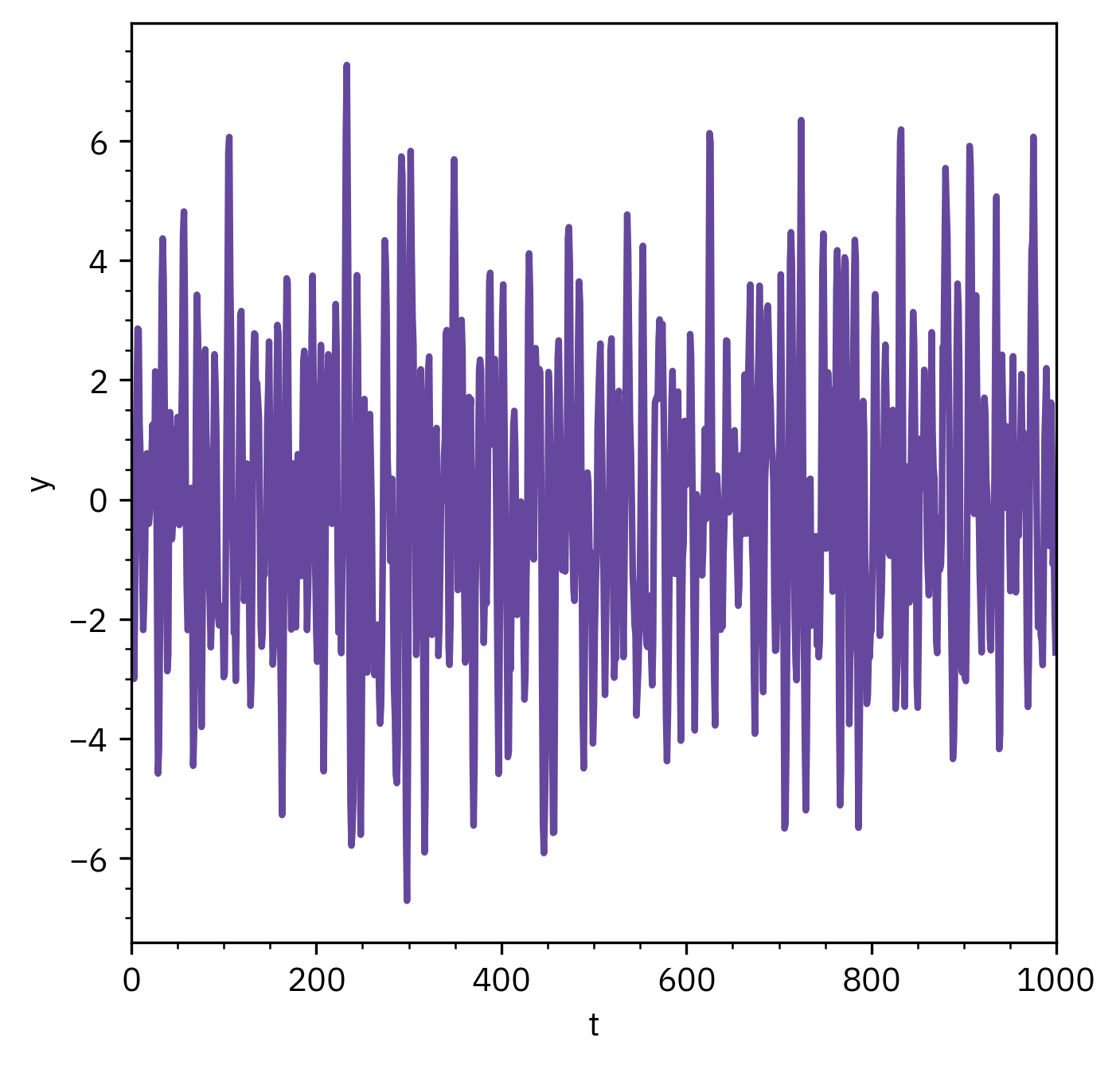
Time series Modelling and analysis

Advanced Modeling and Control

Outline

  • Introduction & Motivation
  • Basics of Time Series
  • Transfer Function Models
  • Autoregressive (AR) Models
    • ARX Models
    • ARMAX Models
    • ARMA/ARIMA Models
  • Model Evaluation & Selection
  • Summary & Reflection

What is Time Series?

  • A time series is a sequence of observations recorded at successive points in time
  • Each observation is ordered, meaning the position in time matters
  • Data is often collected at regular intervals:
    • Seconds, minutes, hours (process monitoring sensors)
    • Days, months, years (economic, environmental, health data)

Importance

  • Provides patterns and forecasts to support decisions
  • Anticipates specification violations in process industries
  • Typical applications:
    • Process control
    • Energy demand forecasting
    • Equipment health monitoring
    • Economic and financial trends
    • Climate and agriculture planning
    • Public health surveillance

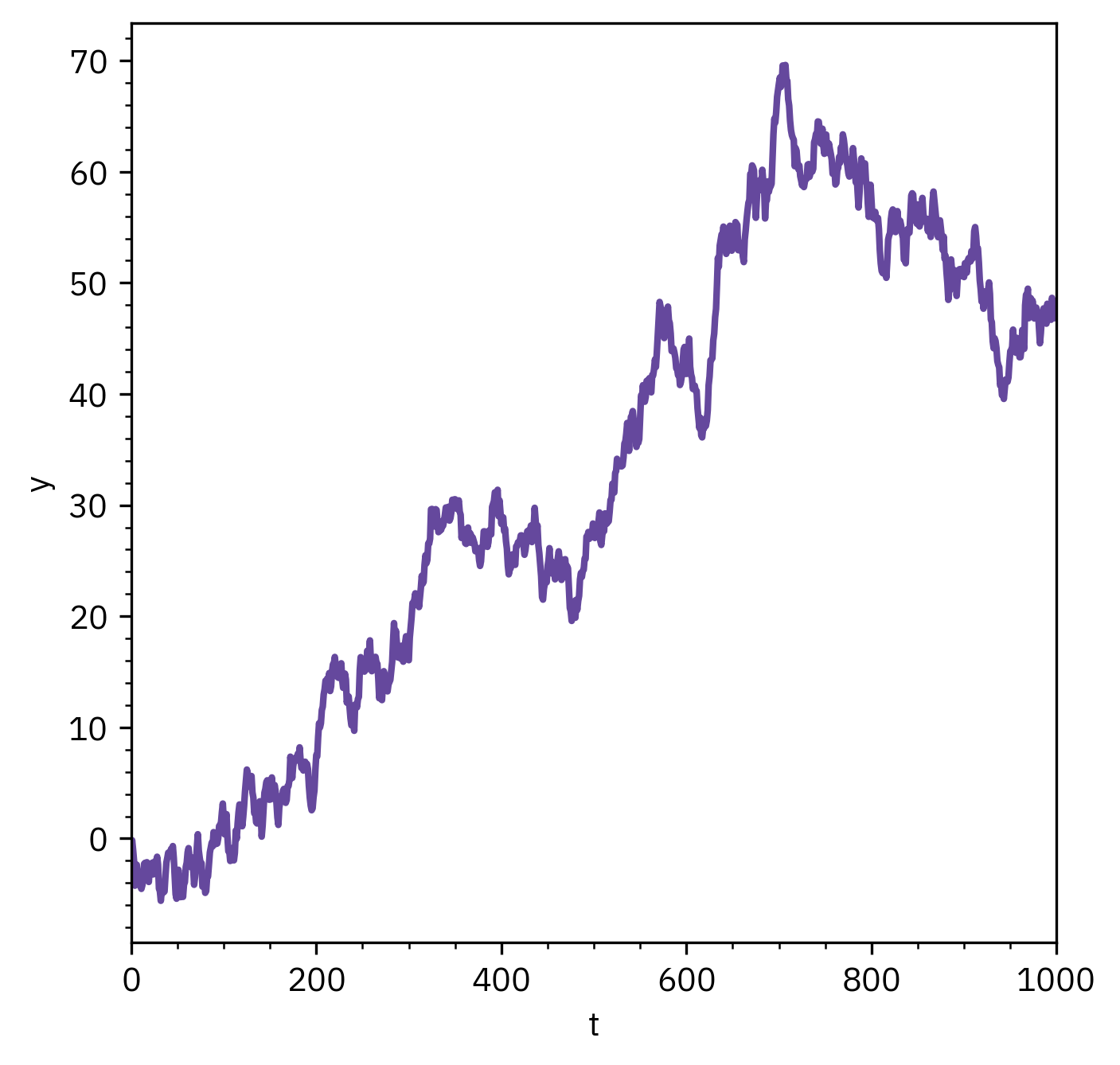
Stationary vs Non-stationary

Stationary series

  • Mean and variance constant over time
  • Fluctuates around a stable level
  • Easier to model and forecast

Non-stationary series

  • Mean or variance changes with time
  • Shows trend, seasonality, or shifts
  • Requires differencing or detrending

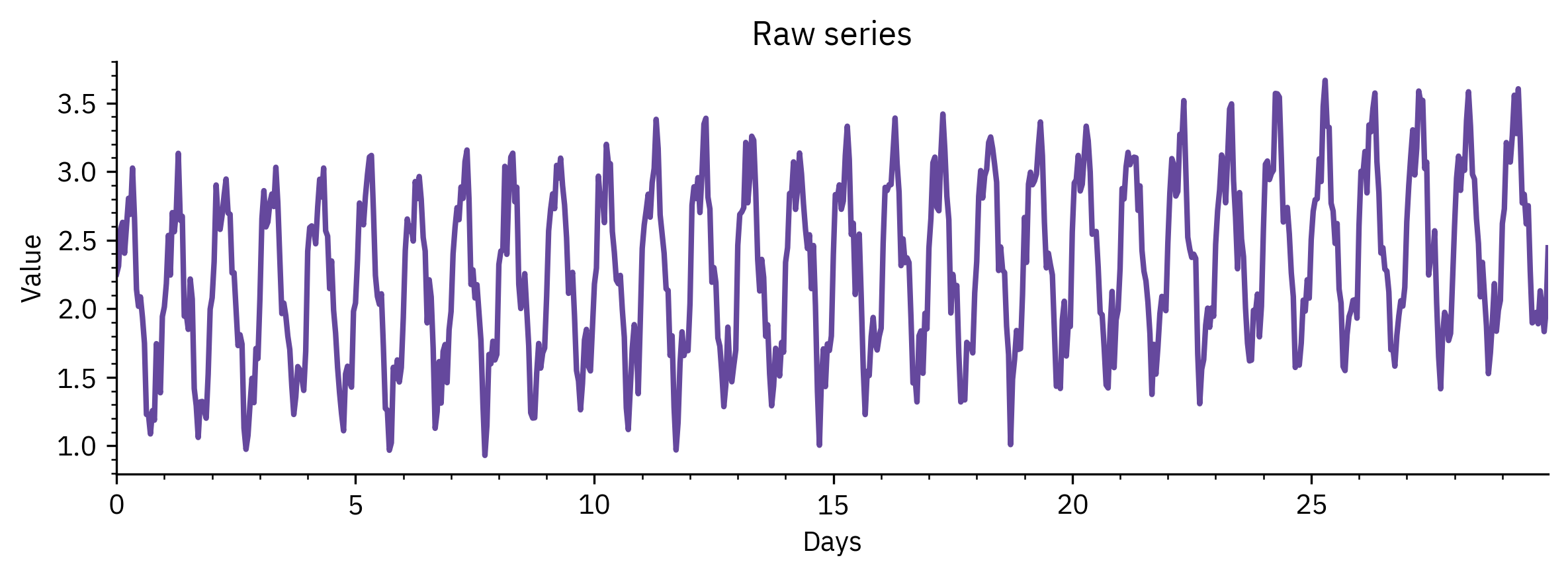
Time Series Representation

  • Time series often large and high-dimensional
  • Representation helps simplify analysis and comparison
  • Common approaches:
    • Raw series (original data)
    • Resampling (reducing data points, e.g., daily → monthly)
    • Transformation (Fourier, wavelets, PCA)
    • Symbolic representation (grouping values into categories)

Benefits

  • Reduces dimensionality while preserving essential patterns
  • Enables efficient similarity search and clustering
  • Provides basis for further tasks:
    • Pattern discovery, Classification, Forecasting

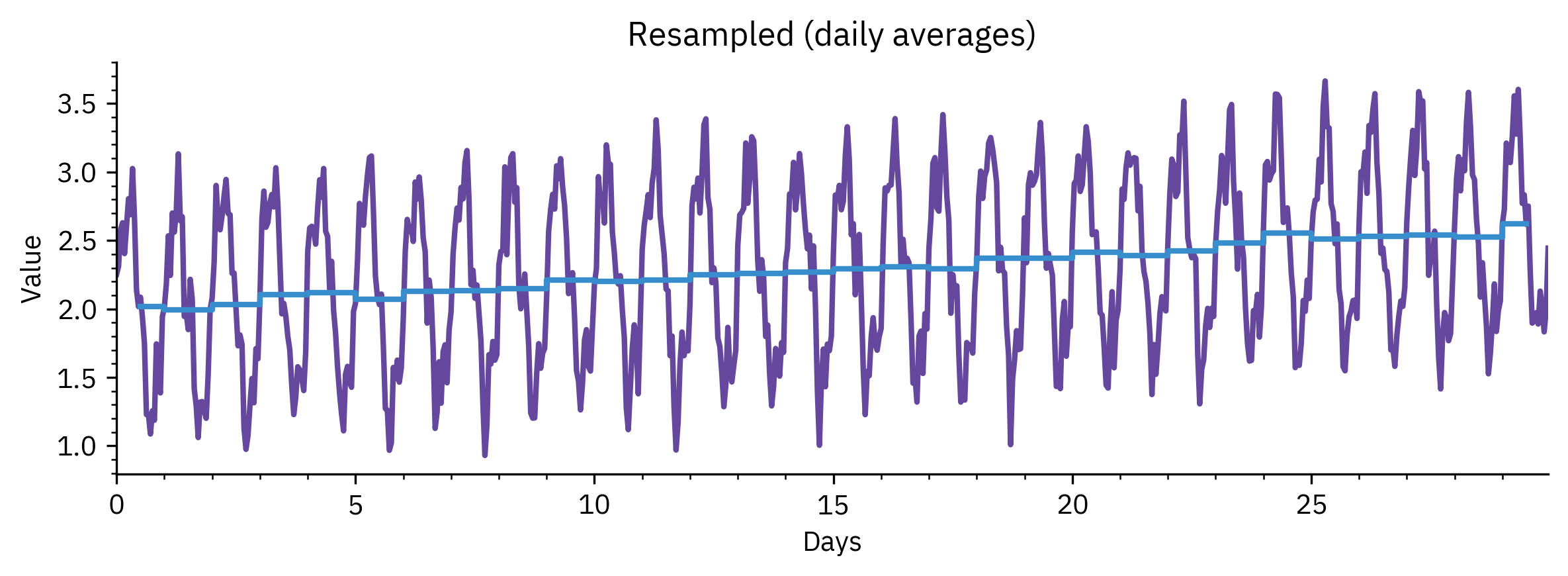
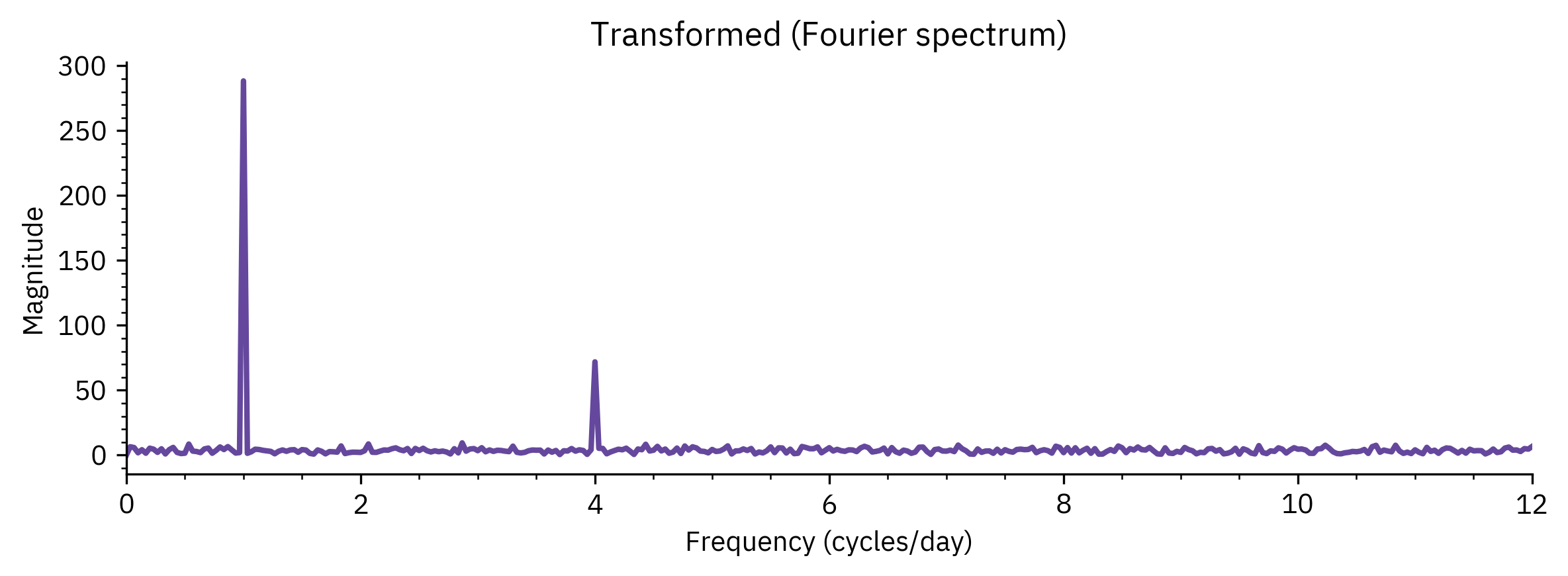
Similarity Measures

  • Used to compare two or more time series
  • Important for:
    • Clustering and classification
    • Pattern discovery
    • Anomaly detection
  • Common measures:
    • Euclidean distance
    • Correlation-based distance
    • Dynamic Time Warping (DTW) for misaligned series

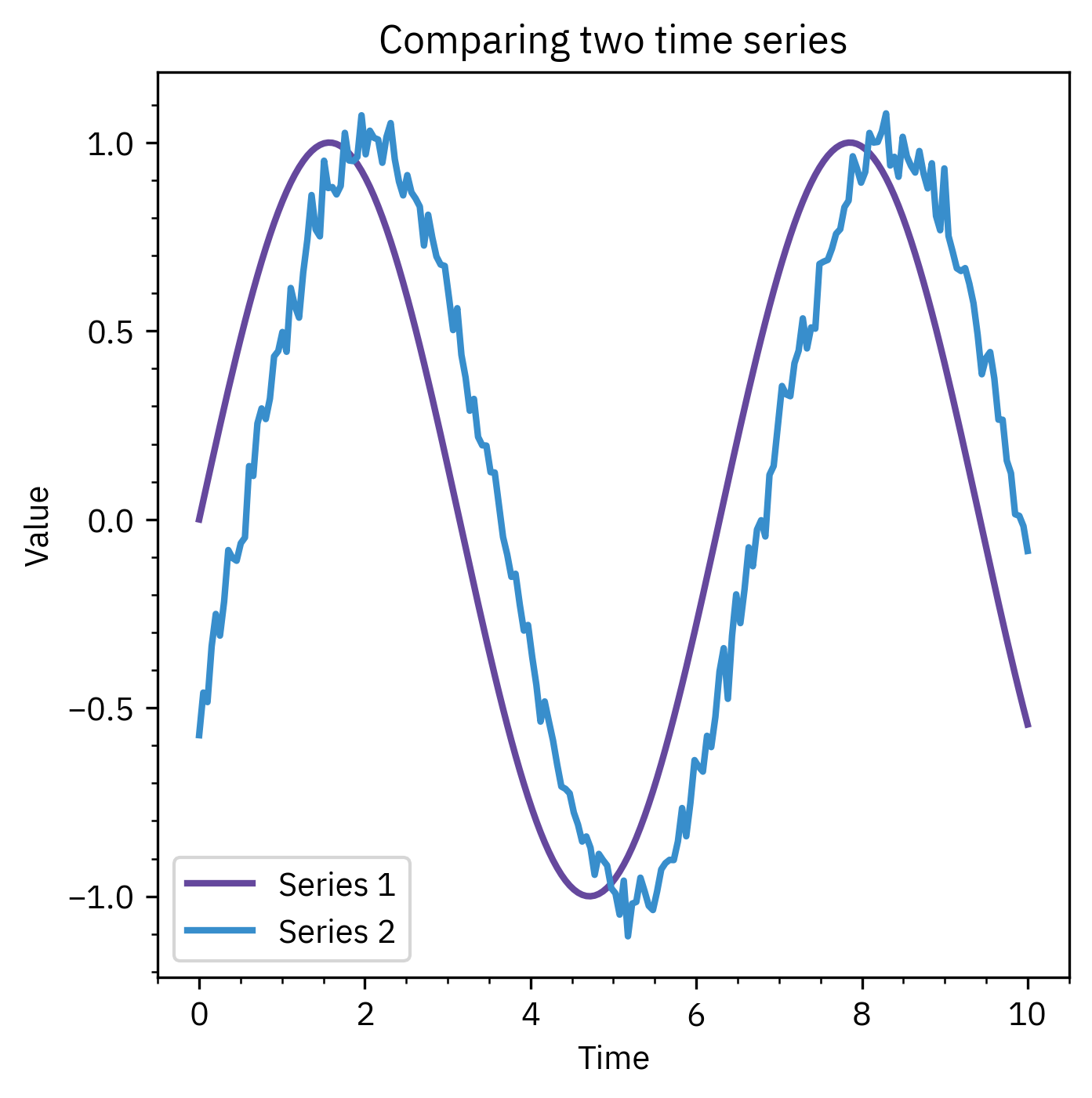
  • Euclidean distance works if sequences are aligned
  • DTW allows matching when sequences are stretched or shifted
  • Correlation-based measures capture shape similarity
  • Choice of similarity measure affects clustering, anomaly detection, and forecasting

Characteristics of Time Series

  • Temporal dependence: current values often depend on past values
  • Directionality: useful for forecasting forward in time
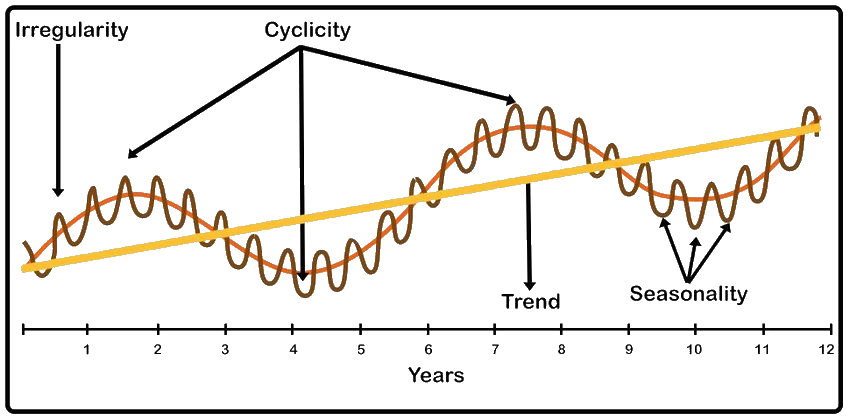
  • Patterns may include:
    • Trend (long-term increase or decrease)
    • Seasonality (repeated cycles, e.g., daily, monthly, yearly)
    • Random fluctuations (noise)

Time-Series Decomposition

  • A time series can be expressed as the sum of underlying components
    • Trend: long-term direction
    • Seasonality: repeating cycles
    • Cyclic variation: slower, irregular fluctuations
    • Residual: noise or unexpected shocks

Mining in Time Series

  • Goal: discover hidden information or patterns
  • Common tasks:
    • Pattern discovery and clustering
    • Classification (e.g., healthy vs faulty sensor data)
    • Rule discovery (if X happens, Y follows)
    • Summarization and anomaly detection

These tasks often rely on similarity measures, representation, and decomposition.

What Do We Mean by Modelling?

  • A model is a simplified description used to explain and predict data
  • Two perspectives:
    • Structural: parameters have physical meaning (equation / transfer function)
    • Data-driven: parameters capture patterns (e.g., neural network)
  • What models enable: simulation, forecasting, pattern recognition

flowchart TD
    A["Time series data"]
    B["Structural model<br/>(equation / TF)"]
    C["Data-driven model<br/>(neural network)"]
    D["Outcomes<br/>• Simulation<br/> • Forecasting<br/>• Pattern recognition"]

    A --> B
    A --> C
    B --> D
    C --> D

    %% IBM Carbon color tokens
    %% Blue 60, Green 60, Purple 60, Magenta 60, Gray 90 text
    classDef data      fill:#65489d,stroke:#65489d,color:#ffffff;

    %% color=['#65489d', '#388ecc', '#105e5d', '#9f1d54', '#4d1013']

    class A data;
    class B data;
    class C data;
    class D data;

    %% Subtle thicker links, orthogonal/top-down feel
    linkStyle default stroke:#525252,stroke-width:2px

Structural vs Data-Driven Models

Structural models

  • Based on physical laws and first principles
  • Parameters have physical interpretation
  • Examples:
    • Transfer functions
    • Differential equations

Pros: interpretability, extrapolation
Cons: need detailed knowledge

Data-driven models

  • Based on observed data patterns
  • Parameters capture correlations, not physics
  • Examples:
    • AR, ARX, ARMAX
    • Neural networks

Pros: flexible, captures complex patterns
Cons: less interpretable, may overfit

Transfer Function Models

  • Many physical processes can be represented by transfer functions in the Laplace domain
  • Transfer function relates input → output dynamics
  • Useful for:
    • Capturing process gain, time constant, and delay
    • Providing a baseline for time-series model comparison
  • Often estimated from input–output data (system identification)

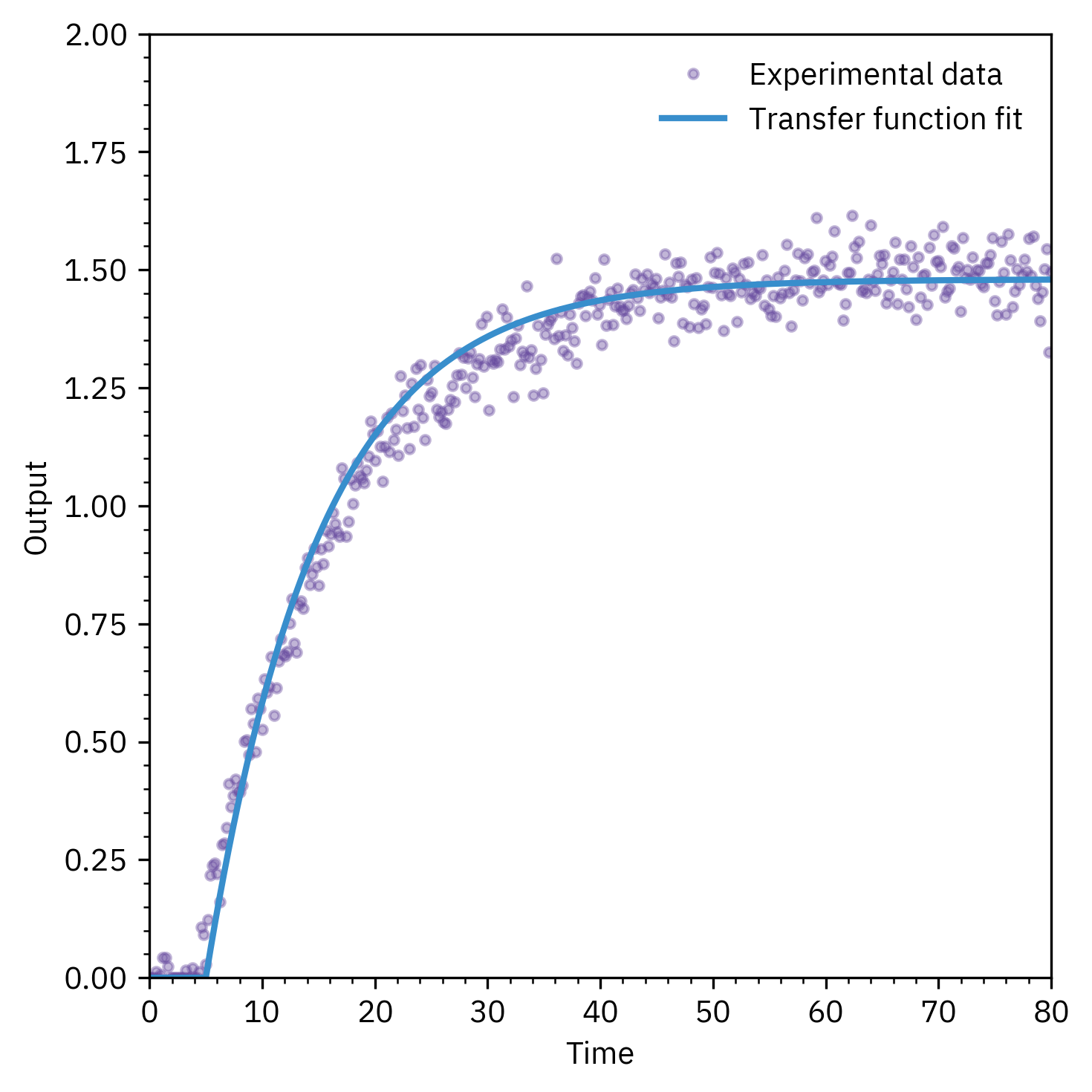
Transfer Functions as a Starting Point

  • Physics-based intuition: order, delay, stability
  • Provides initial guess for data-driven models (ARX, ARMAX)
  • Bridges between first-principles modeling and time-series modeling

Activity 1: Estimating Transfer Function Models for a Heat Exchanger.

Autoregressive (AR) Models

  • Concept
    • Current value depends on a linear combination of past values
    • AR(p):
      y_t = \phi_1 y_{t-1} + \phi_2 y_{t-2} + \dots + \phi_p y_{t-p} + e_t
    • Captures short-term correlations in stationary data
  • MATLAB
    • ar(data, order) estimates AR model
    • Order selection via AIC / FPE
  • Applications
    • Forecasting short horizon
    • Identifying dominant lags
    • Noise modeling in ARMAX

Autoregressive (AR) Models

  • Present value depends on past values in discrete time

  • General AR(n):

    y_t = c + \sum_{i=1}^n \alpha_i y_{t-i} + \varepsilon_t

    • Where: c: constant; \alpha_i: AR coefficients; n: model order; \varepsilon_t: white noise

  • Example for AR(2):

    y_t = c + \alpha_1 y_{t-1} + \alpha_2 y_{t-2} + \varepsilon_t

  • Properties of AR models

    • Short-term memory, good for capturing autocorrelation
    • Flexible building block for ARX, ARMAX, ARIMA

AR model with backshift operator z^{-k}

  • AR(2) in operator notation:

    y_t = c + \alpha_1 y_{t-1} + \alpha_2 y_{t-2} + \varepsilon_t

    can be written as

    (1 + \alpha_1 z^{-1} + \alpha_2 z^{-2}) y_t = c + \varepsilon_t

    y_t = \frac{c + \varepsilon_t}{1 + \alpha_1 z^{-1} + \alpha_2 z^{-2}} \,=\, \frac{c + \varepsilon_t}{A(z)}

  • Interpretation

    • The AR model acts like a filter that takes in random noise and produces the series.

    • The filter has only poles (all-pole system), so the effect of a shock gradually fades but never ends completely (infinite impulse response, IIR).

    • In contrast, some models have responses that die out completely after a fixed time (finite impulse response, FIR).

In-class Activity 2

Fit an AR model to Australia COVID-19 infection data (Australia_covid_cases.xlsx) and evaluate order selection.

ARX Models

  • ARX: Autoregressive with Exogenous Input

  • Exogenous Input

    • Many processes are driven by outside factors (inputs, e.g. manipulated variables, disturbances)
    • In a distillation column, the feed composition or coolant flow are exogenous inputs that affect the impurity (output).
    • In finance, the interest rate might be an exogenous input affecting stock prices.

    👉 Exogenous input = something external you can measure and that drives the system.

  • Why ARX?

    • AR models only use past outputs → good for forecasting trends
    • ARX extends AR by including the exogenous inputs explicitly

ARX Model

Structure

A(q^{-1}) y(t) = B(q^{-1}) u(t-n_k) + e(t) - A(q^{-1}): polynomial in past outputs
- B(q^{-1}): polynomial in past inputs
- n_k: input delay
- e(t): noise

  • Interpretation
    • Captures cause–effect between input and output
    • Useful for system identification with I/O data

MATLAB

m = arx(data, [na nb nk])
where na = AR order, nb = input order, nk = input delay.

Activity 3: Develop an ARX Model for a Given Transfer Function

ARMA Models

  • ARMA: Autoregressive Moving Average
    • AR models capture dependence on past outputs
    • But sometimes random shocks persist for several steps (noise is not white)
    • ARMA = AR + MA, adds a moving average (MA) term for noise

Structure

A(q^{-1}) y(t) = C(q^{-1}) e(t) - A(q^{-1}): polynomial in past outputs
- C(q^{-1}): polynomial in past noise (MA part); e(t): white noise

  • Interpretation
    • Models a stationary time series without external input
    • Captures both memory in outputs and persistence in shocks
    • Building block for ARIMA models (to handle non-stationarity)

MATLAB

m = arima(p,0,q)
where p = AR order, q = MA order.
Use estimate(m, data) to fit.

ARMAX Models

  • ARMAX: Autoregressive Moving Average with Exogenous Input
    • ARX models assume the disturbance is white noise
    • In practice, noise often has its own dynamics (colored noise)
    • ARMAX extends ARX by adding a moving average (MA) term for noise

Structure

A(q^{-1}) y(t) = B(q^{-1}) u(t-n_k) + C(q^{-1}) e(t) - A(q^{-1}): past outputs; B(q^{-1}): past inputs (exogenous input)
- C(q^{-1}): noise dynamics (MA part); n_k: input delay

  • Interpretation
    • Captures both input–output dynamics and structured noise
    • More flexible and realistic than ARX
    • Often needed when residuals of ARX show correlation

ARIMA Models

  • ARIMA = Autoregressive Integrated Moving Average
  • Extends ARMA for non-stationary series

    • Integration differencing step

      \nabla y(t) = y(t) - y(t-1)

    • Makes the series stationary before ARMA modeling

  • Interpretation
    • AR: memory of past values
    • I: removes trends and seasonality
    • MA: corrects random shocks

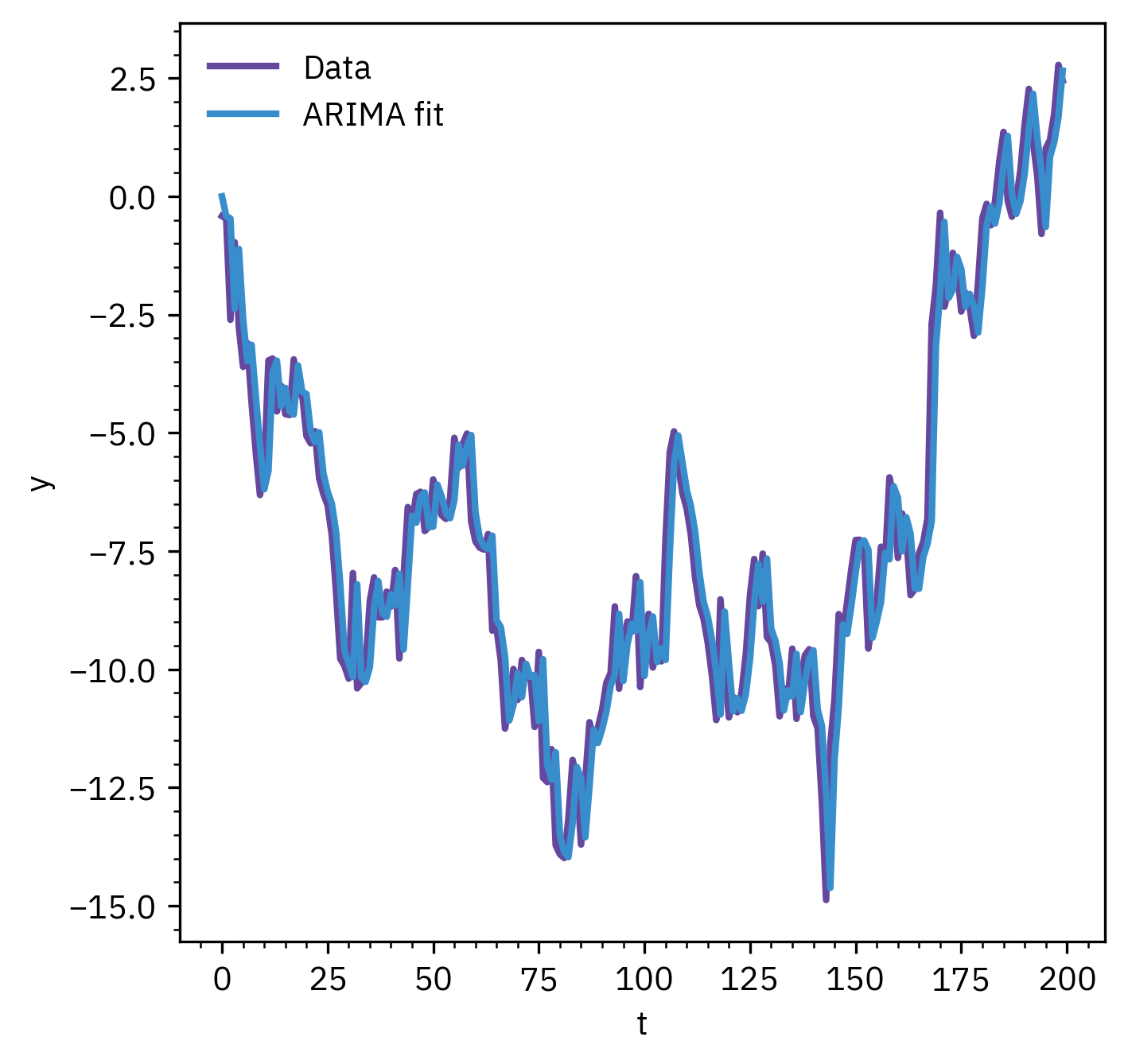
MATLAB

m = arima(p,d,q)
p = AR order; d = number of differences (integration order); q = order of MA part

Activity 4: Iron Ore Prices – ARIMA Modeling

Model Evaluation and Selection

  • Many possible models → need criteria to choose the best one

  • Avoid overfitting (too complex) and underfitting (too simple)

  • Common criteria

    • Residual analysis (should look like white noise)
    • Goodness of fit (%) to validation data
    • Information criteria (Akaike information criteria (AIC), Final prediction error (FPE))
    • Prediction accuracy (on test data)

  • Best practice

    • Compare several models with different orders
    • Choose the simplest model that explains the data well
    • Validate with unseen (test) data if available

In MATLAB

  • goodnessOfFit
  • compare(data, model1, model2, ...) → compare fit visually
  • aic, fpe → return information criteria
  • resid(data, model) → check residuals

Summary

  • Time-series data can be broken into components: trend, seasonality, cyclic variation, and residuals
  • Models help us explain and predict time-series behavior
    • AR models: depend on past outputs
    • ARX models: extend AR by including exogenous inputs
    • ARMA/ARMAX: combine autoregression with moving average, noise modeling
    • ARIMA: adds differencing for non-stationary data
  • Model evaluation and selection
    • Check residuals (should look like white noise)
    • Use metrics like AIC, FPE, fit percentage
    • Validate using unseen data

📌 Different models suit different needs — forecasting, simulation, or understanding system dynamics.