Primary loop analysis
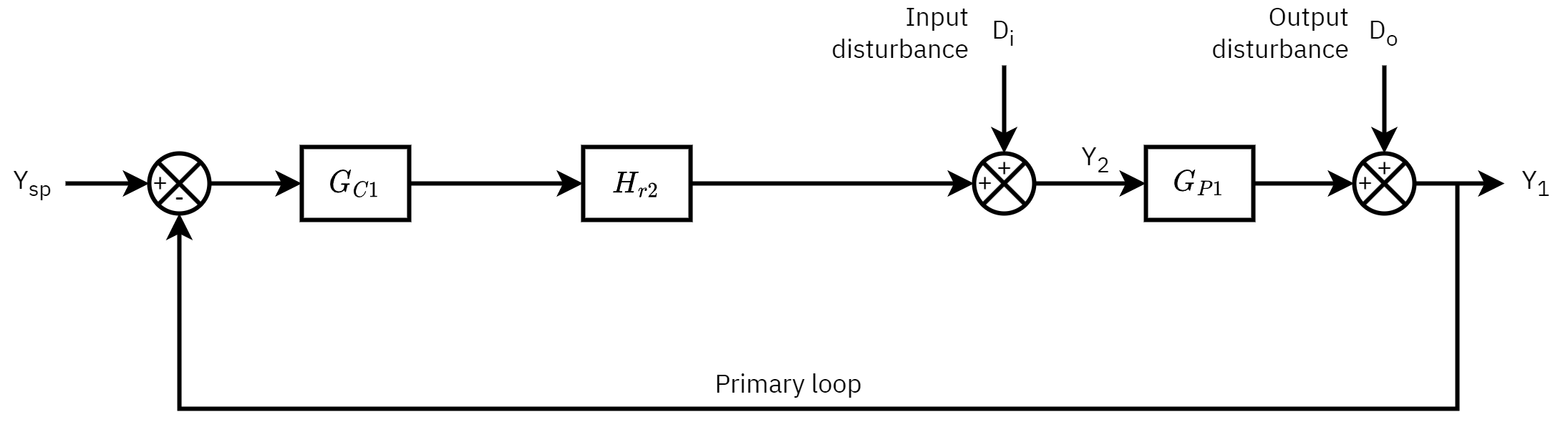
- Augmented primary process
- is used to design or tune the primary controller. This means that the secondary controller should be designed first, as the primary design depends on the .
Advanced Modeling and Control
In cascade control, we have one manipulated variable and more than one measurement.
Key features:
The disturbance must has an effect on the secondary measurement
Causal (cause-and-effect) relationship between the secondary measurement and manipulated variable
Causal relationship between the manipulated variable, and between secondary and primary measurements.
Secondary loop must be faster than the primary loop
Open loop stable Gp=τs+1Kpe−θs
Integrating Gp=sKpe−θs
Open loop unstable Gp=τs−1Kpe−θs
PI controller Gc=Kc(1+τIs1)
PID controller (Ideal) Gc=Kc(1+τIs1+τDs)
PID controller (Parallel) Gc=Kc+Is1+D1+Ns1N
Primary process Gp1=τ1s+1Kp1e−θ1s
Secondary process Gp2=τ2s+1Kp2e−θ2s
Primary controller Gc=Kc(1+τIs1)
Secondary controller Gc=Kc
Setpoint transfer function Hr2=1+GC2GP2GC2GP2
Characteristic equation 1+GC2GP2=0
1+τ2s+1KC2KP2e−θ2s=0
Let Loop gain KL2=KC2KP2
Delay: e−θ2s≊1−θ2s
Characteristic Polynomial τ2s+1+KL2(1−θ2s)=0
a1(τ2−KL2θ2)s+a0(1+KL2)=0
Necessary stability criterion: a1>0,a0>0
Upper limit on the loop gain
a1=τ2−KL2θ2>0;∴KL2=θ2τ2
lower limit on the loop gain
a0=1+KL2>0;∴KL2>−1
Since the lower limit is negative, due to practical reason the minimum value of loop gain should be above 0 but lower than its upper limit. Thus, for stability the loop gain is given as
KL2=Rp2(θ2τ2);0<Rp2<1
The parameter RP2 can be used to tune the controller gain as: KC2=Kp2Rp2θ2τ2
Hr2=τc2s+1KOexp(−θ2s);where, Ko=1+KL2KL2,τc2=1+KL2τ2
Notice that KL2=Rp2θ2τ2
Therefore, overall gain and closed-loop time constant can be written as Ko=θ2+Rp2τ2Rp2τ2;τc2=θ2+Rp2τ2θ2τ2
To increase the speed of response of secondary controller, increase the value of Rp2 but keep the value below 1 to ensure stability.
Gpa=Hr2Gp1≅τ1s+1KoKp1e−(θ1+θ2+τc2)s
The effect of input disturbance is given by Hd2
Hd2=τc2s+1KD0;KD0=1+KL21=θ2+Rp2τ2θ2
Primary setpoint transfer function Hr1:
Hr1=1+Gc1Hr2Gp1Gc1Hr2Gp1
Characteristic equation (CE):
1+Gc1Hr2Gp1=0;1+τIs(τ1s+1)Kc1K0Kp1(τIs+1)e−θts=0
where, θt=θ1+θ2+τc2
Let loop gain KL1=KC1K0Kp1 and e−θts≊1−θts
Simplifying CE to polynomial
τIs(τ1s+1)+KL1(τIs+1)(1−θts)=0
a2τI(τ1−KL1θt)s2+a1τI+KL1(τI−θt)s+a0KL1=0
Necessary stability criterion requires a2>0,a1>0, and a0>0
These provide the limits for loop gain KL1
To ensure stability, the loop gain must be bounded between its minimum upper limit and maximum lower limit
Provides tuning parameters for the controller
There should be a well-defined relation between the primary and secondary measured variables.
Essential disturbances should act in the inner loop.
The inner loop should be faster than the outer loop. The typical rule of thumb is that the average residence times should have a ratio of at least five.
It should be possible to have a high gain in the inner loop.
Cascade control can be used when there are several measurement signals and one control variable.
It is particularly useful when there are significant dynamics, e.g., long dead times or long time constants, between the control variable and the process variable.
Tighter control can then be achieved by using an intermediate measured signal that responds faster to the control signal.

Advanced Modeling and Control