Feedforward and ratio control

Advanced Modeling and Control

Feedback control advantages

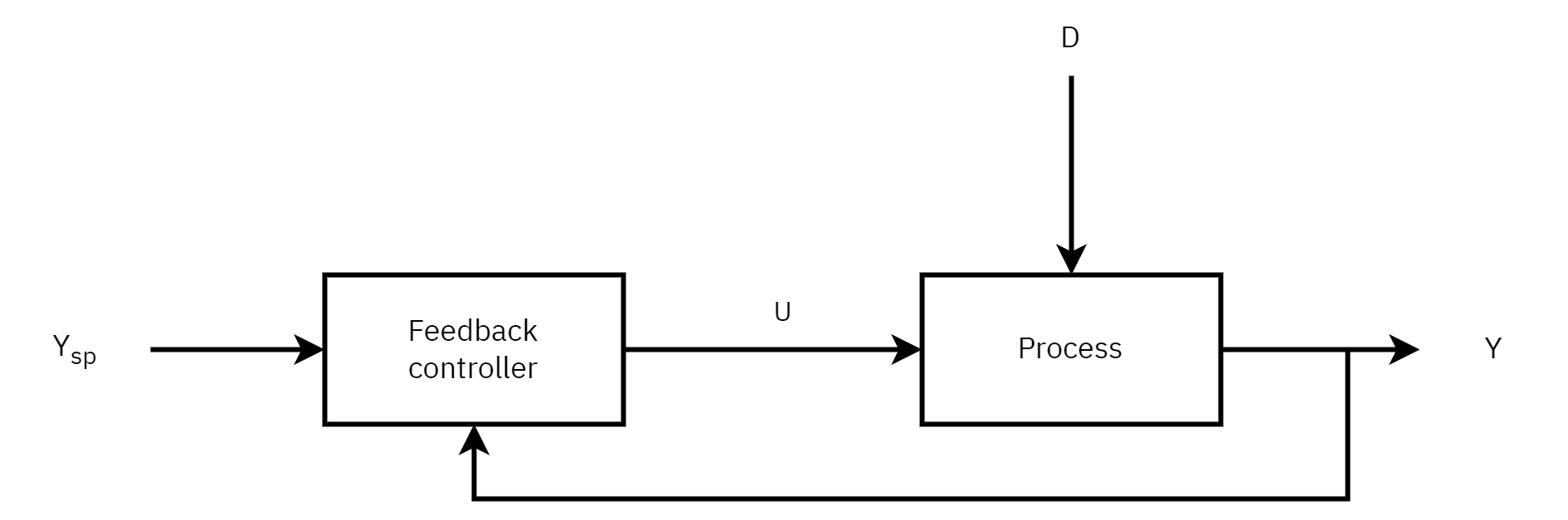
• Corrective action occurs as soon as the controlled variable deviates from the set point, regardless of the source and type of disturbance.

• Feedback control requires minimal knowledge about the process to be controlled; in particular, a mathematical model of the process is not required, although it can be very useful for control system design.

• The ubiquitous PID controller is both versatile and robust. If process conditions change, re-tuning the controller usually produces satisfactory control

Feedback control disadvantages

• No corrective action is taken until after a deviation in the controlled variable occurs. Thus, perfect control, where the controlled variable does not deviate from the set point during disturbance or set-point changes, is theoretically impossible.

• It does not provide predictive control action to compensate for the effects of known or measurable disturbances.

• It may not be satisfactory for processes with large time constants and/or long time delays. If large and frequent disturbances occur, the process may operate continuously in a transient state and never attain the desired steady state.

• In some situations, the controlled variable cannot be measured on-line, so feedback control is not feasible.

For situations in which feedback control by itself is not satisfactory, significant improvement can be achieved by adding feedforward control. But feedforward control requires that the disturbances be measured (or estimated) on-line.

Introduction to feedforward control

• The basic concept of feedforward control is to measure important disturbance variables and take corrective action before they upset the process.

• In contrast, a feedback controller does not take corrective action until after the disturbance has upset the process and generated a nonzero error signal.

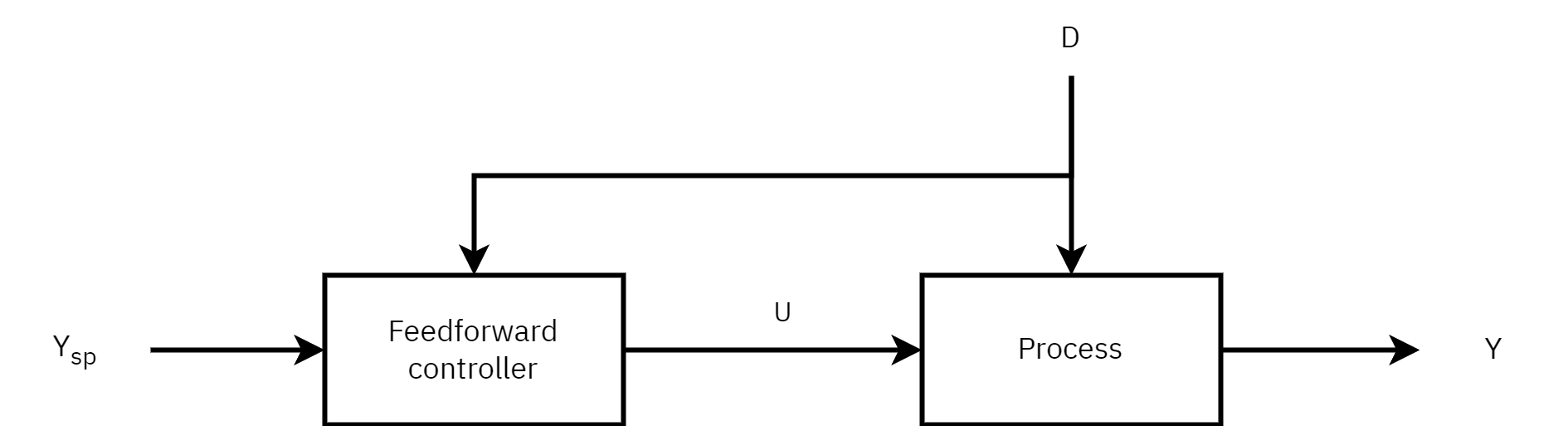
Comparison between
feedforward and feedback control

Feedforward control

Advantages

• Acts before the disturbance reaches the process
• Cannot cause instability
• Good for slow process dynamics

Disadvantages

• Must identify and measure all disturbances
• Fails for unmeasured disturbances
• Relies on availability of process models
• No indication of control quality

Feedback control

Advantages

• No disturbance measurements needed
• No process model necessary
• Can cope with changes within process

Disadvantages

• Will always have some transient error
• Poor for slow dynamics and interactions
• Instability is possible

Feedforward control configuration

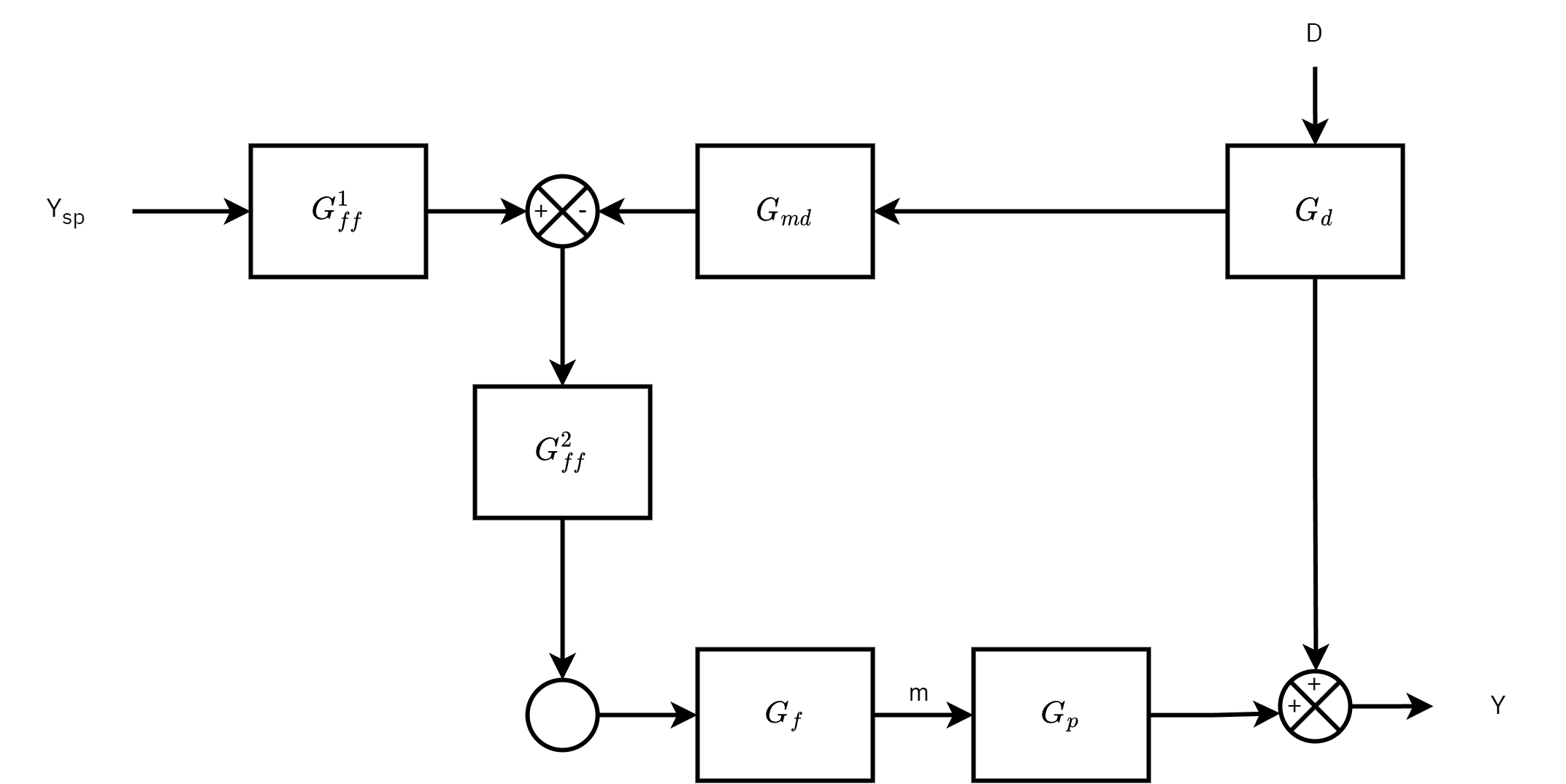
Feedforward control configuration

• Transfer functions G^1_{ff} = \frac{G_{md}}{G_d}; G^2_{ff}=-\frac{G_d}{G_p G_f G_{md}}

• Neglecting dynamics of final control element and sensor

G^1_{ff} = \frac{1}{G_d}; G^2_{ff}=-\frac{G_d}{G_p}

Sometimes idealized feedforward controller cannot be realized physically due to non-causal system

Non-causal idealized feedforward controller

Consider

G_d = \frac{2 e^{-3s}}{5s + 1}

G_p = \frac{e^{-5s}}{2s + 1}

Idealized feedforward controller

G_{ff} = -\frac{G_d}{G_p} = -\frac{2(2s+1)e^{2s}}{5s+1}

Not realizable due to the predictive term e^{2s}

Consider

G_d = \frac{e^{-2s}}{s + 1}

G_p = \frac{e^{-s}}{s^2 + 2s + 1}

Idealized feedforward controller

G_{ff} = -\frac{G_d}{G_p} = -\frac{(s^2 + 2s + 1) e^{-s} }{s+1}

Not realizable because the numerator order is higher than the denominator

Feedforward-Feedback control configuration

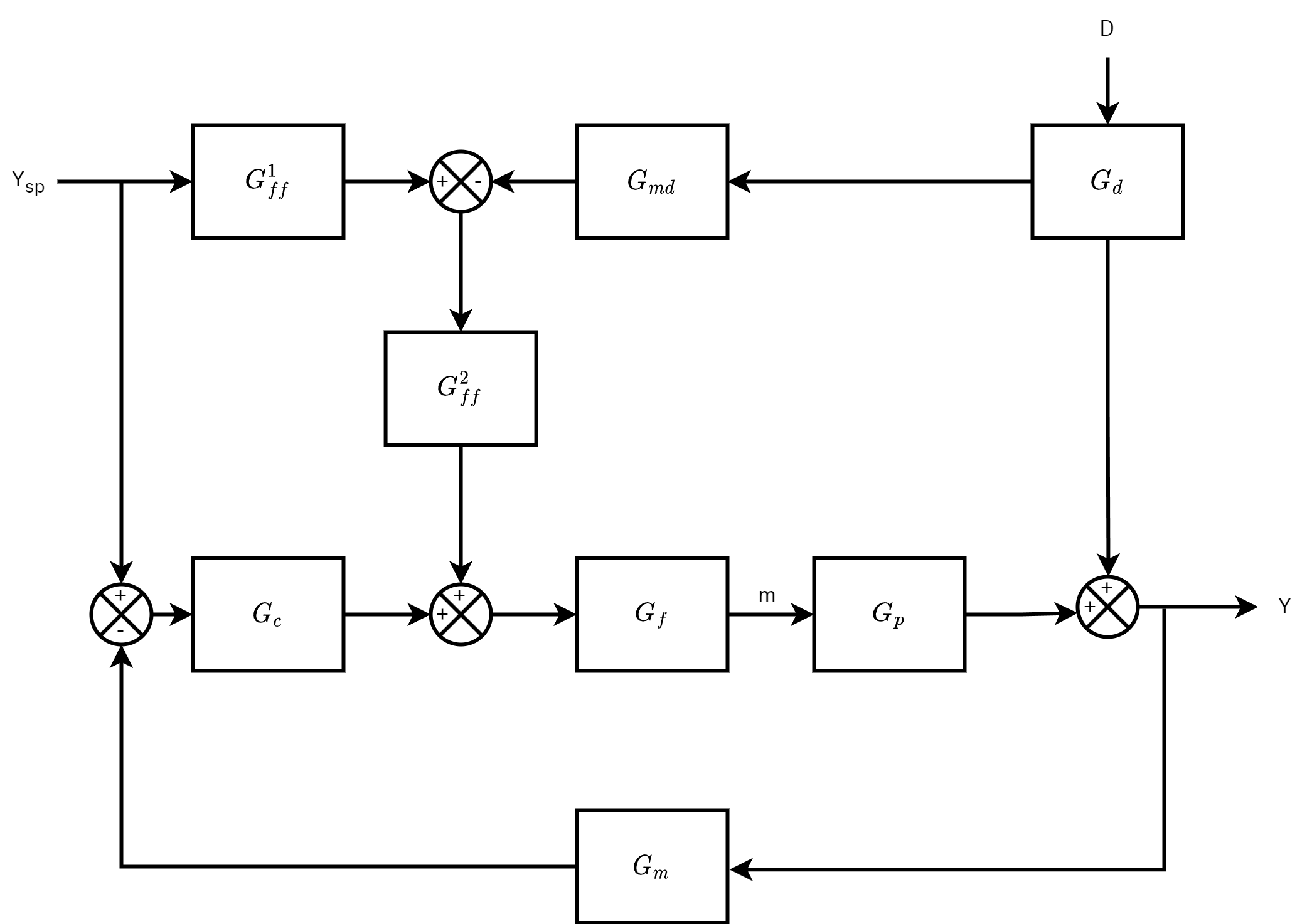
Feedforward-Feedback control configuration

• Closed loop transfer function

\begin{split} y(s) = & \frac{G_p G_f [G^2_{ff} G^1_{ff} + G_c]}{1 + G_p G_f G_c G_m} y_{sp}(s) \\[1ex] & + \frac{G_d - G_p G_f G^2_{ff} G_{md}}{1 + G_p G_f G_c G_m} d(s) \end{split}

• Characteristic equation for this closed-loop system

1 + G_p G_f G_c G_m = 0

Ratio control

Ratio control is a special type of feedforward control that has had widespread application in the process industries. Its objective is to maintain the ratio of two process variables at a specified value. The two variables are usually flow rates, a manipulated variable u and a disturbance variable d. Thus, the ratio u/d is controlled rather than individual variables.

R := \frac{u}{d}

Typical applications

1. specifying the relative amounts of components in blending operations.

2. maintaining a stoichiometric ratio of reactants to a reactor.

3. keeping a specified reflux ratio for a distillation column.

4. holding the fuel-air ratio to a furnace at the optimum value.

Ratio control schemes

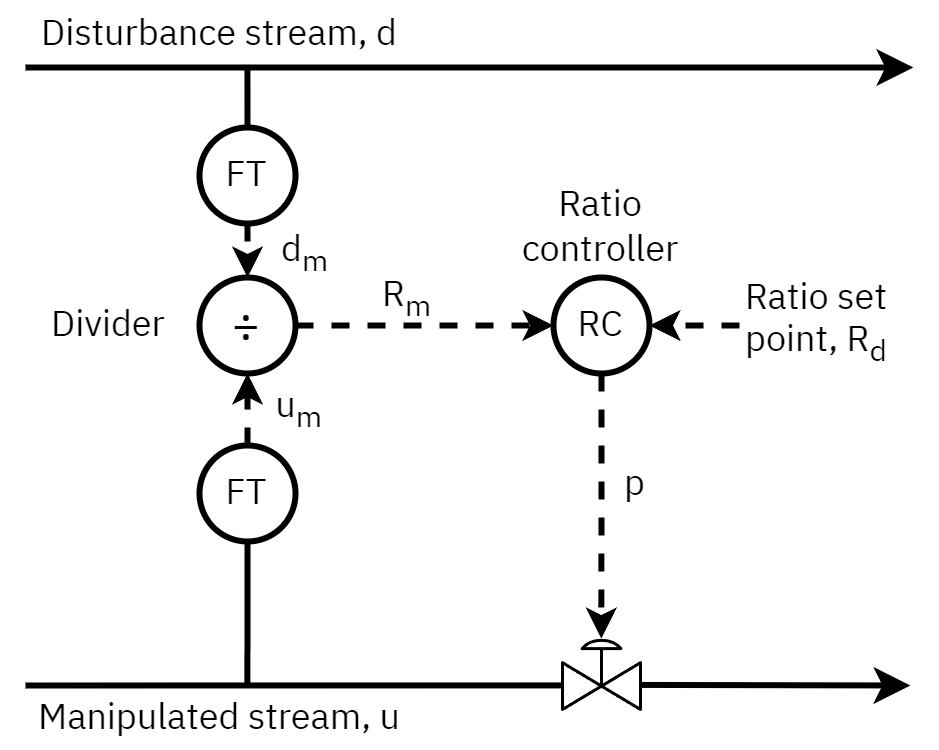
Method 1

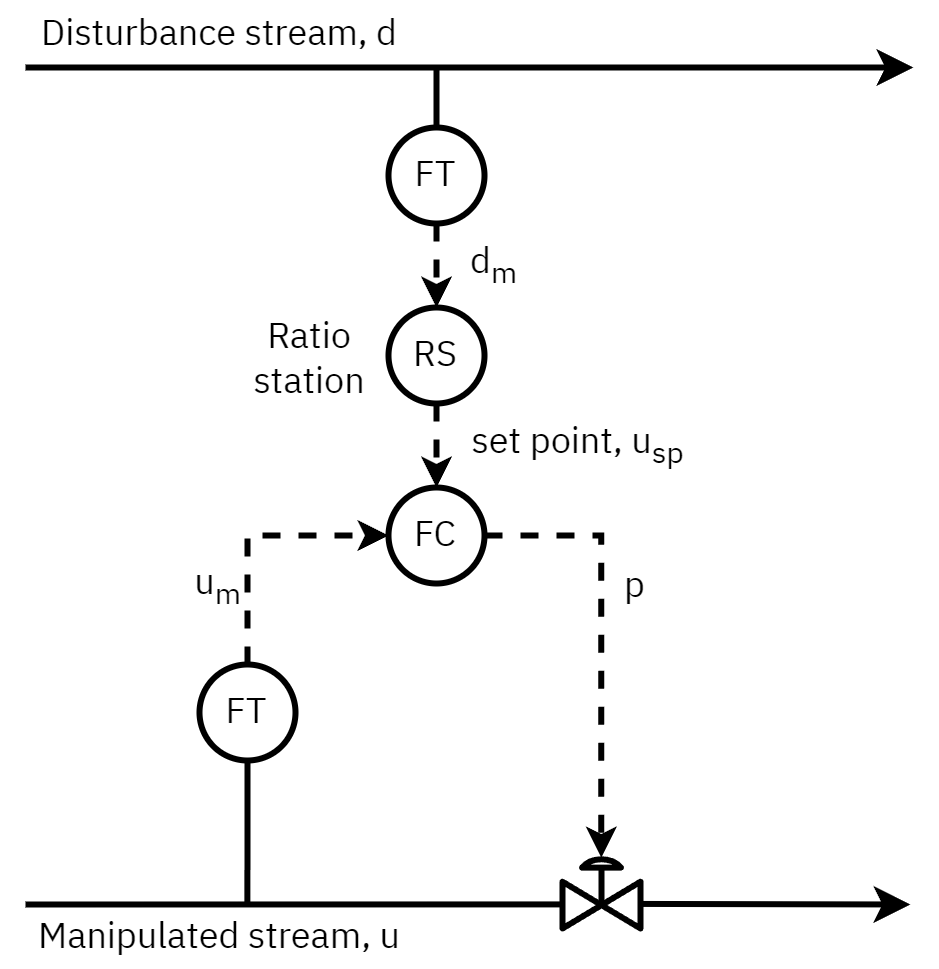
Method 2

Stability

• While feedback control is inherently stable due to its self-correcting nature, feedforward control requires careful consideration of system stability.

• Unstable behavior can arise in feedforward control systems due to modeling errors or incorrect estimation of disturbance effects.

• When combined with feedback control, the feedback loop can often correct these stability issues. However, if the feedforward control is dominant, it might destabilize the system.

• In the design phase, engineers should thoroughly test the system response to various disturbances to ensure stability.

Tuning feedforward controllers

• Tuning a feedforward controller involves adjusting the gain and two time constants: lead and lag.

• The lead time constant helps the controller anticipate rapid changes, and the lag time constant allows it to respond to slow disturbances. Proper tuning ensures a balance between fast response and system stability.

• Tuning is often achieved through simulation or experimental methods.

• Gain scheduling can be used to adjust controller parameters based on system conditions.

• When combined with feedback control in a two-degree-of-freedom control structure, the feedback controller compensates for the feedforward controller’s imperfections, ensuring overall system stability.